Extensive experiments on four multi-view datasets
are conducted to demonstrate the effectiveness of
the proposed framework.
1.2 Organization
The remainder of this paper is organized as follows: We
present a general feature-level framework for completing
missing view to obtain the integrated representations for
multi-view data in Section 2.1. In Section 2.2, a novel Iso-
morphic Linear Correlation Analysis model is developed
for correlating different views through learning a set of
excellent isomorphic features. We build a new Identical Dis-
tribution Pursuit Completion model to recover missing
view of multi-view data under both semantic complemen-
tarity and identical distribution restraints in Section 2.3. Fur-
thermore, Section 3 provides an efficient algorithm to solve
the proposed framework and analyzes the computational
complexities and convergence rates of the proposed algo-
rithms. Section 4 gives a broad overview of some related
work. Experimental results and analyses are reported in
Section 5. Section 6 concludes this paper.
1.3 Notations
Here we establish some notations to be used throughout
this paper. Assume V
x
and V
y
are two different views. Let
the data matrices X
E
¼½x
1
; ...;x
n
1
T
2 R
n
1
d
x
and Y
E
¼
½y
1
; ...;y
n
1
T
2 R
n
1
d
y
be two sets of existing heterogeneous
representations from the V
x
and V
y
, respectively, where
x
i
2 R
d
x
is the ith sample from V
x
, y
i
2 R
d
y
is the ith sample
from V
y
, n
1
is the number of available samples, and d
x
and
d
y
are the dimensionalities of the heterogeneous low-level
feature spaces V
x
and V
y
. Note that for i ¼ 1; ...;n
1
, ðx
i
;y
i
Þ
represents the ith couple of heterogeneous representations.
We assume that both fx
i
g
n
1
i¼1
and fy
i
g
n
1
i¼1
are centered, i.e.,
P
n
1
i¼1
x
i
¼ 0 and
P
n
1
i¼1
y
i
¼ 0. Let the data matrix X
M
¼
½x
n
1
þ1
; ...;x
n
1
þn
2
T
2 R
n
2
d
x
be a set of missing representa-
tions from the V
x
and the data matrix Y
M
¼½y
n
1
þ1
; ...;
y
n
1
þn
2
T
2 R
n
2
d
y
be a set of existing heterogeneous repre-
sentations from the V
y
corresponding to the missing repre-
sentations X
M
.
We use jjAjj
¼
P
r
i¼1
s
i
to denote the trace (nuclear)
norm of a matrix A ¼½a
ij
2R
pq
, where r ¼ rankðAÞ
denotes the rank of A and fs
i
g
r
i¼1
is the set of singular val-
ues of A in a non-increasing order. jjAjj
F
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
P
p
i¼1
P
q
j¼1
a
2
ij
q
is the Frobenius norm of A.IfA is a square matrix, then let
trðAÞ¼
P
p
i¼1
a
ii
be the trace of A. For two matrices A and
B, hA; Bi¼trðA
T
BÞ denotes the matrix inner product. For a
vector b 2 R
p
, let jjbjj
2
¼
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
P
p
i¼1
b
2
i
p
be the ‘
2
-norm of b.
Additionally, let jHj be the number of elements in the set
H; ÏfðCÞ denotes the gradient of any smooth function fðÞ
at the point C; for w 2 R
p
, we denote by diagðwÞ the diago-
nal matrix having the components of the vector w on the
diagonal; let D be a set of representations, meanðDÞ denotes
the average value of D. I
k
2 R
k
is an identity matrix.
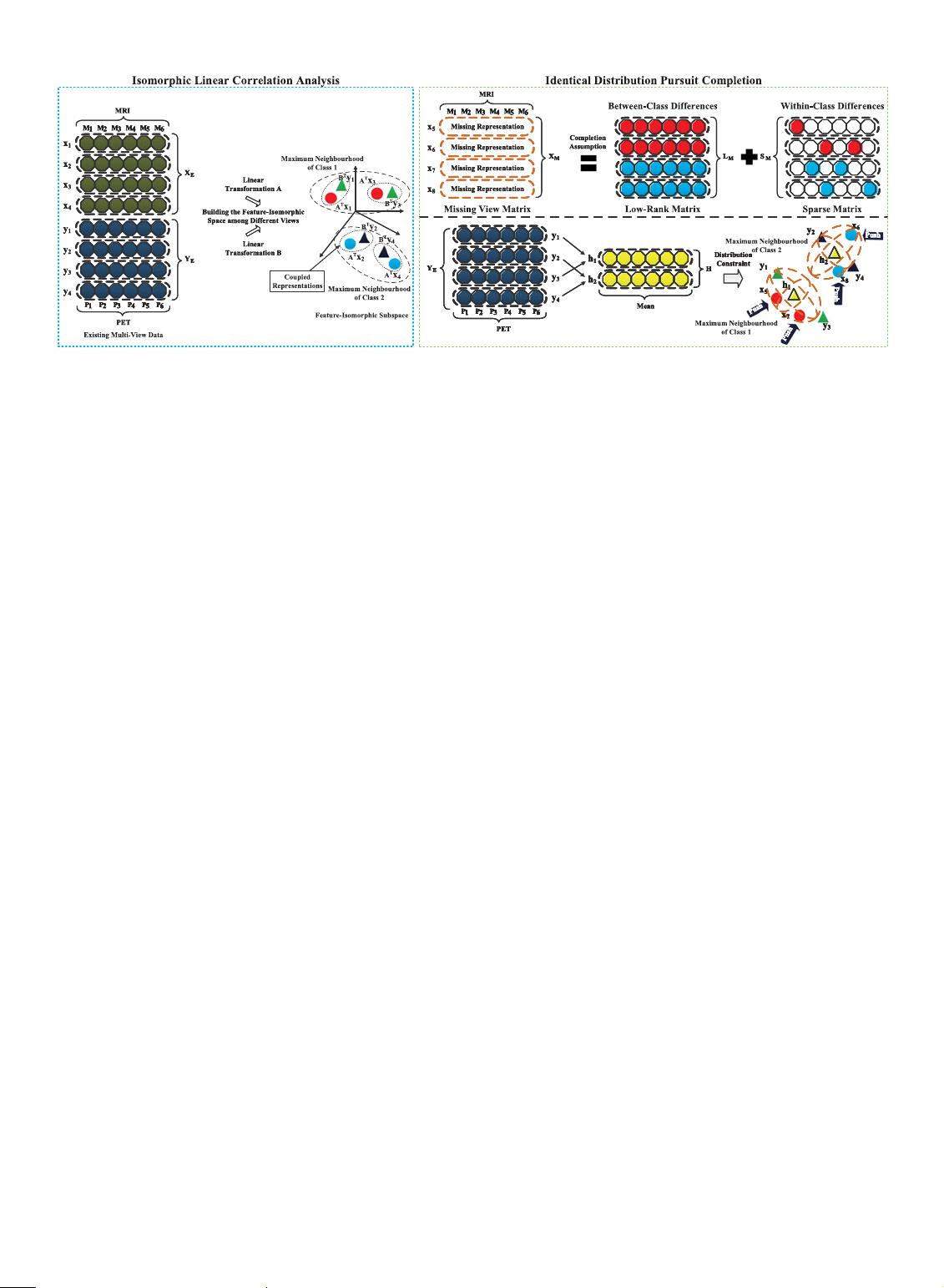
2THE PROPOSED FORMULATION
We propose a general feature-level framework to complete
missing view of multi-view data. A graphical illustration of
the proposed formulation is given in Fig. 4 to facilitate the
understanding the proposed formulations and algorithms
significantly.
2.1 Overview of the Proposed Formulations
We provide an overview of the proposed formulations by
using the example in Fig. 4. In this example, a set of multi-
view data consists of the views MRI and PET. However, the
MRI view is missing, such as all attributes in the representa-
tions x
5
, x
6
, x
7
, and x
8
are totally absent.
To recover missing view of multi-view data, a feature-
isomorphic subspace is learned by ILCA model to build a
bridge between multiple heterogeneous low-level feature
spaces in the proposed framework, in which the same
dimension and attributes are used to represent the same
semantic concept. Specifically, to fully exploit both semantic
complementarity and similar distributions among different
views as shown in Fig. 3, multiple linear transformations A
and B are learned using the existing multi-view data X
E
and Y
E
to eliminate the heterogeneity across them. Thus, a
feature-isomorphic subspace is obtained by a set of learned
excellent isomorphic features, in which the correlated repre-
sentations from different views are coupled together to
capture the commonality among the heterogeneous repre-
sentations from different views. Consequently, some maxi-
mum neighbourhoods are established among different
categories, such as the maximum neighbourhoods of Class
1 and Class 2 in Fig. 4. We can measure the correlation
among the multi-view data in the feature-isomorphic
Fig. 4. The proposed framework for completing missing view of multi-view data.
1298 IEEE TRANSACTIONS ON KNOWLEDGE AND DATA ENGINEERING, VOL. 30, NO. 7, JULY 2018









