6西格玛质量控制：数据处理与Statistical软件分析

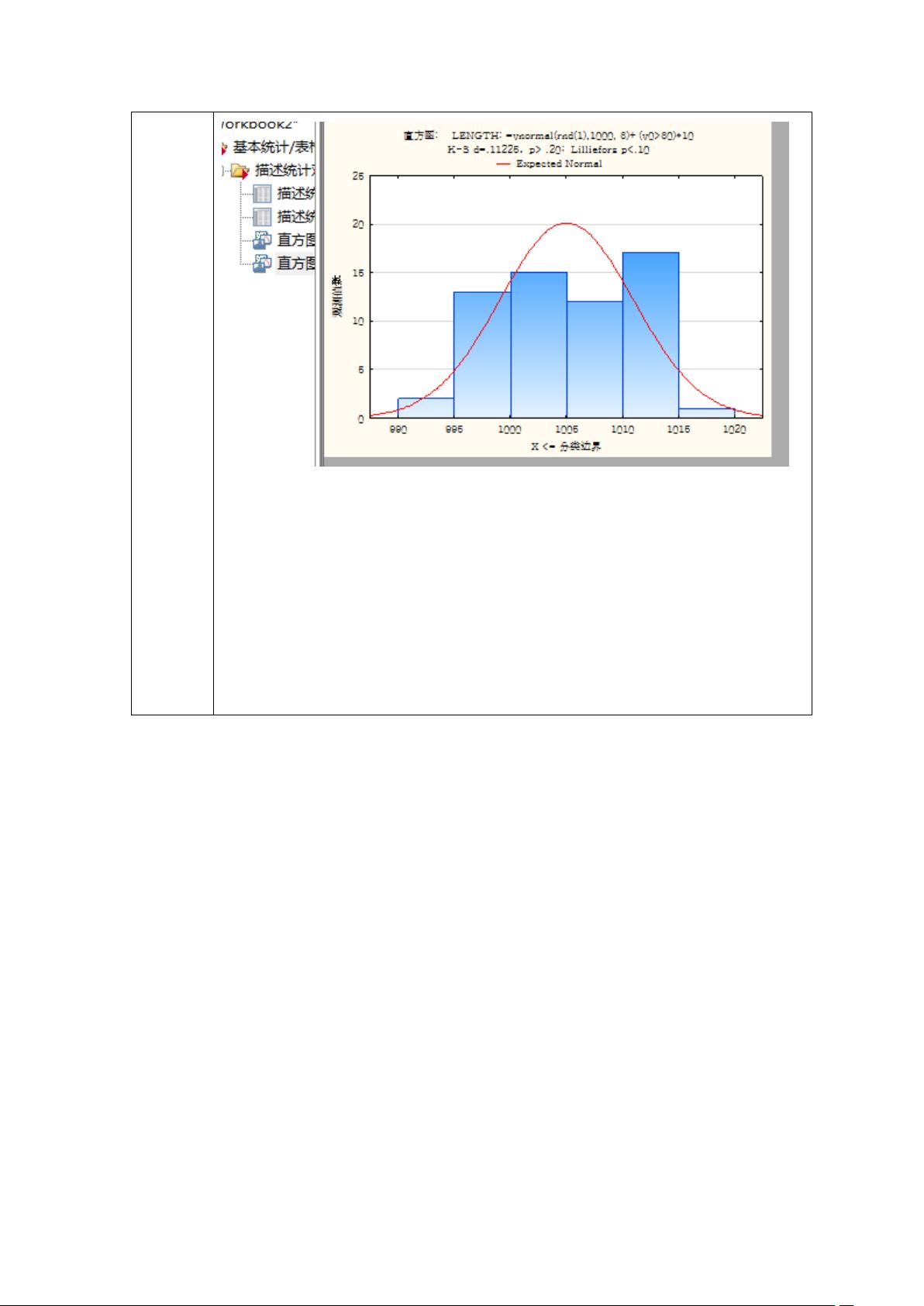
"该文档是关于6西格玛质量控制的数据处理与分析的教程，源自理学院《试验设计及质量控制》课程的实验报告。实验时间为2013年12月11日，旨在让学习者掌握6西格玛过程、Statistical软件的运用以及如何在该软件环境下进行数据处理和分析，包括描述统计、直方图、箱线图和假设检验（单样本t检验和两独立样本t检验）。" 在6西格玛质量控制中，数据处理和分析是至关重要的环节，它帮助我们识别和改进过程中的缺陷，以达到近乎完美的产品质量。实验内容首先介绍了描述统计，包括计算变量的均值、中位数、标准差、最小值、最大值和极差，这些指标提供了数据集的基本特征。Statistical软件被用来执行这些计算，简化了数据分析的过程。 接着，实验展示了如何利用软件绘制直方图，这是一种可视化工具，能直观地展示数据分布的形状和集中趋势。通过观察直方图，可以判断数据是否接近正态分布或其他类型分布，这对于后续的统计分析非常关键。 此外，箱线图（盒须图）也是6西格玛中常用的工具，用于显示数据的五数概括（最小值、下四分位数、中位数、上四分位数、最大值），它可以清晰地展示数据的离群值和分布范围，对于理解数据的变异性和异常情况非常有用。 实验还涉及了假设检验，首先是单样本t检验，用于比较观测数据与已知标准值的差异。在这个例子中，比较的是百公里耗油量是否显著改变了。如果P值大于显著性水平α（通常取0.05），则无法拒绝原假设，即认为数据并未显示出显著变化。在实验中，P值为0.085808，所以得出结论，百公里耗油量仍为8.48升，没有显著改进。 最后，进行了两独立样本t检验，用于比较两个独立群体的均值差异。同样，如果P值大于α，则两个群体的均值被认为无显著差异。在示例中，由于P值远大于0.05，结论是没有证据表明两组配件厚度的均值存在显著差异。 这个6西格玛实验强调了如何使用统计工具来理解和改进过程质量，通过具体的操作步骤，学生能够深入理解并应用6西格玛方法论，提升其在质量控制领域的实践能力。