离散傅立叶变换(DFT)：核心原理与应用详解

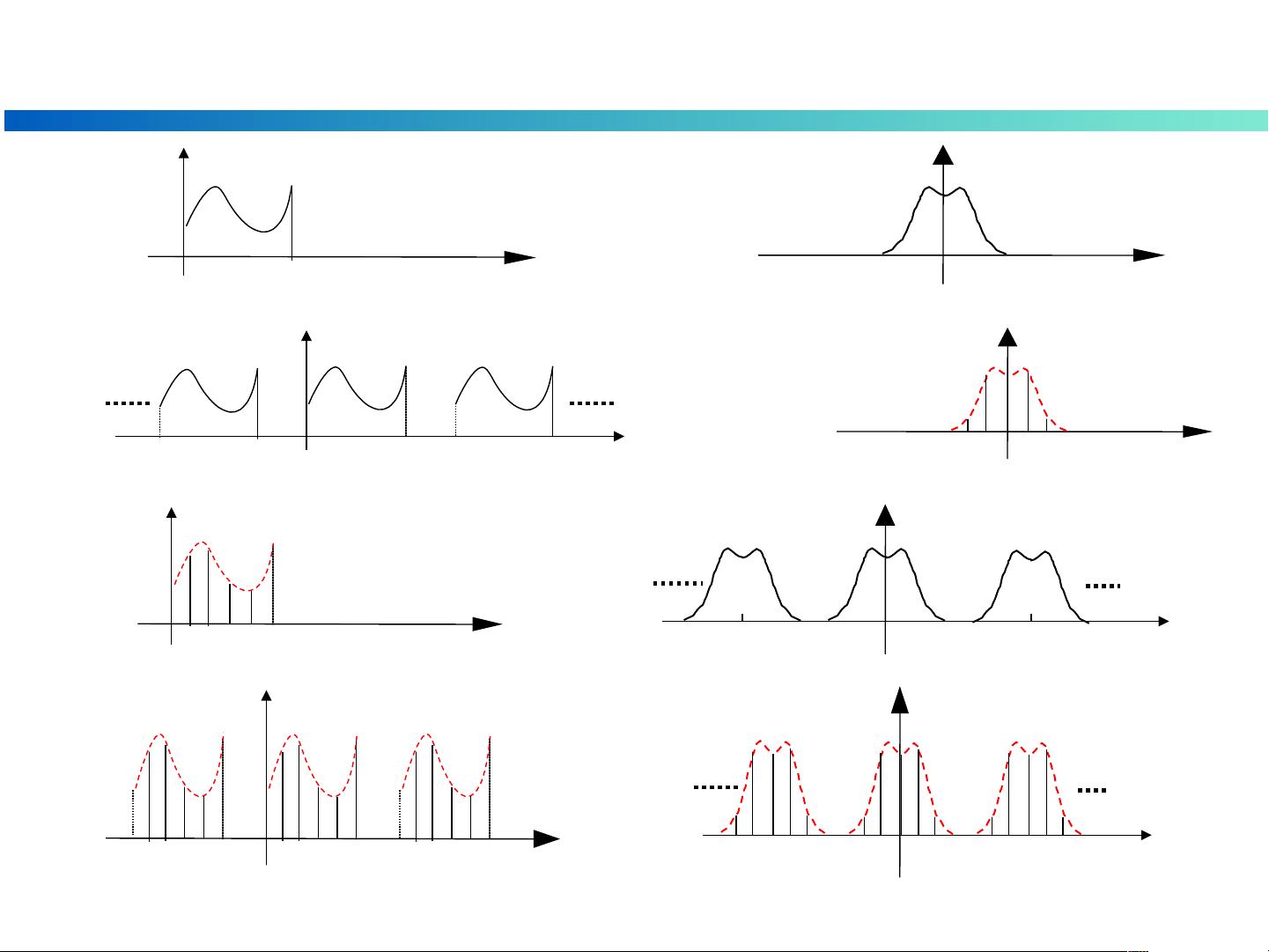
本文档主要介绍了快速傅里叶变换（FFT）的核心原理，以帮助理解信号处理中的基本概念和技术。首先，它阐述了离散傅里叶变换（DFT）的概念，它是从连续信号的傅里叶变换（如傅里叶变换FT和傅里叶级数FS）演变而来的，针对离散时间序列设计。DFT解决了连续变换在计算机上处理的难题，如计算复杂性和信号的无限长度。 DFT的提出源于对离散信号在频域表示的需求，尤其是DTFT（离散时间傅立叶变换）和Z变换。两者虽然都反映了信号的频域特性，但不适合在计算机上直接应用，因为它们涉及的是连续变量。为了解决这个问题，通过在频域采样，即DFS（离散傅立叶级数），并将其推广到有限长度序列，产生了DFT。DFT具有以下关键特点： 1. 有限长序列的离散傅里叶变换：DFT是处理有限长度信号的理想工具，这使得它能够在数字信号处理（DSP）中广泛应用。 2. 可计算性与快速算法：DFT不仅解决了连续信号处理的局限性，还引入了高效的计算方法，如FFT（快速傅立叶变换），极大地提高了计算速度。FFT算法利用了序列的周期性，将计算复杂度从O(n^2)降低到了O(n log n)，对于大规模数据处理极其重要。 本文档详细解释了从DFS和DFT的基本定义、性质，到Z变换与它们的关系，以及DFT如何作为数字信号处理的核心，包括频谱分析的应用。通过对这些概念的理解，读者能够掌握信号处理中的关键步骤和理论基础，为实际应用提供坚实的基础。