小车单摆系统动力学建模与控制器设计

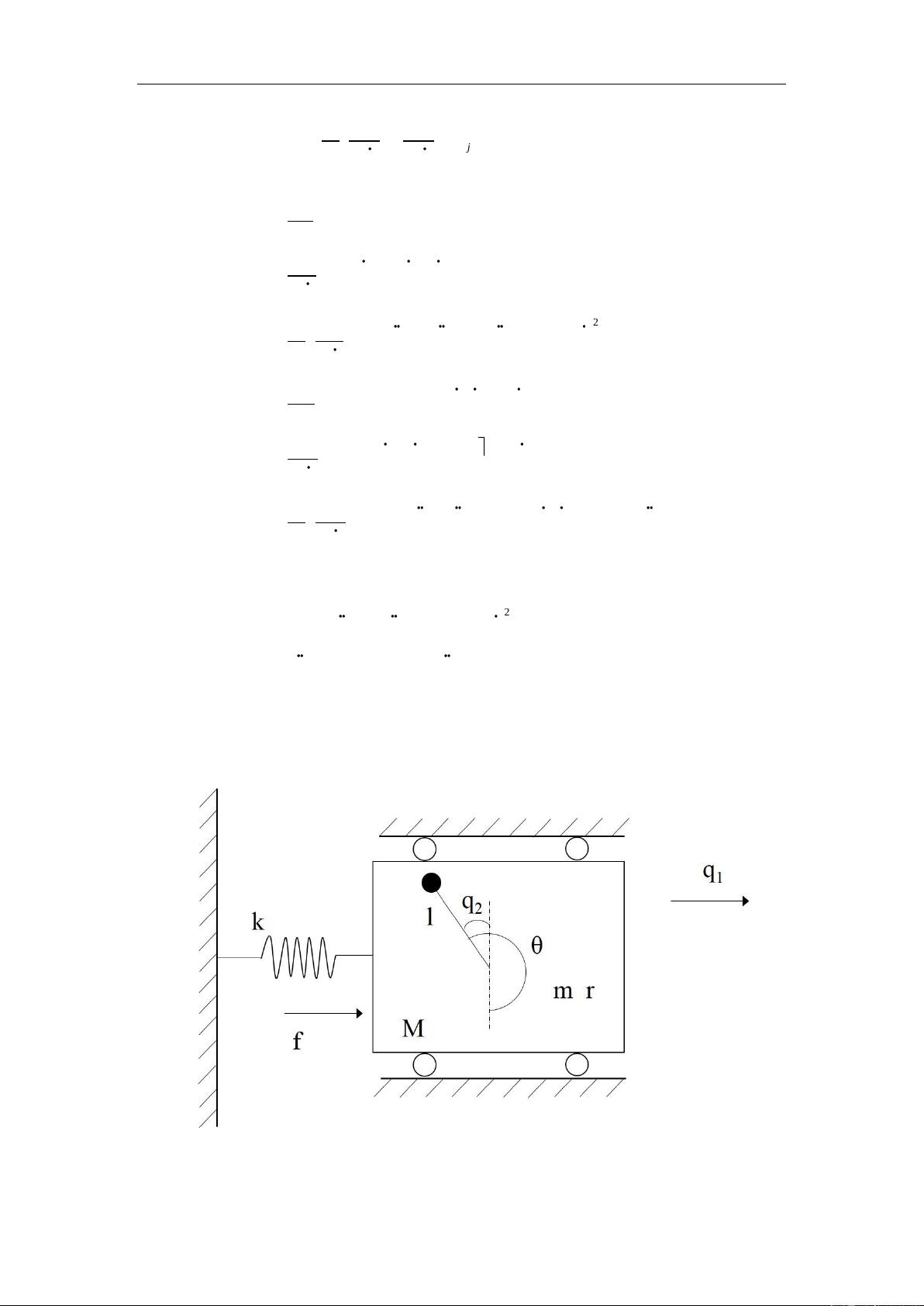
小车单摆系统控制器设计是基于倒立摆技术的一种经典控制系统研究，主要涉及动力学建模、能控性和能观性分析以及稳定控制策略的设计。本文的核心内容如下： 1. 动力学建模：系统由一个小车（质量M=5kg）和一根刚度k=50N/m的弹簧连接到墙壁，一个质量m=0.5kg的钢球通过铰接在小车上，杆长l=0.3m，构成一个倒立摆系统。系统使用小车位置q1和摆动角度q2作为广义坐标。通过计算得到小车的速度v1和摆的速度v2，以及动能T1和T2，包括小车和摆的机械能。拉格朗日函数L定义了系统的总能量，考虑到小车和摆的动能及势能。 2. 稳定性分析：研究了系统在小车内的倒立摆稳定状态下的能控性和能观性。能控性是指系统能否通过外部输入（如力f）完全控制系统的状态，能观性则是指系统状态能否被外部测量完全观察。通过对系统拉格朗日方程的求导和设定外力f，分析了系统固有的自然频率，这对于确保稳定性至关重要。 3. 起摆过程控制：文章关注如何通过合理的力f来实现小车内部摆的起摆，目标是使摆动达到180度并保持稳定。这涉及到对力f的精确计算和控制策略的设计，以克服初始静止状态下的惯性，并在摆动过程中维持动态平衡。 4. 拉格朗日方程的应用：作者运用拉格朗日方程( 1,2) j j j d L L Q j dt q q - ∂L/∂q - ∂L/∂q = ∂L/∂q̇ - ∂L/∂q̈ )的形式来推导动力学方程，其中Q表示广义坐标和它的导数，f是外力的表达式。在这个过程中，还涉及到一些物理量的三角函数关系，如cos和sin。 本文的主要任务是通过建立和分析拉格朗日动力学模型，设计出能够有效控制小车单摆系统，使其能够在稳定状态下起摆并保持预定角度的控制器。这种技术在机器人技术、航空航天等领域有着广泛的应用前景。