使用R软件进行一元线性回归分析

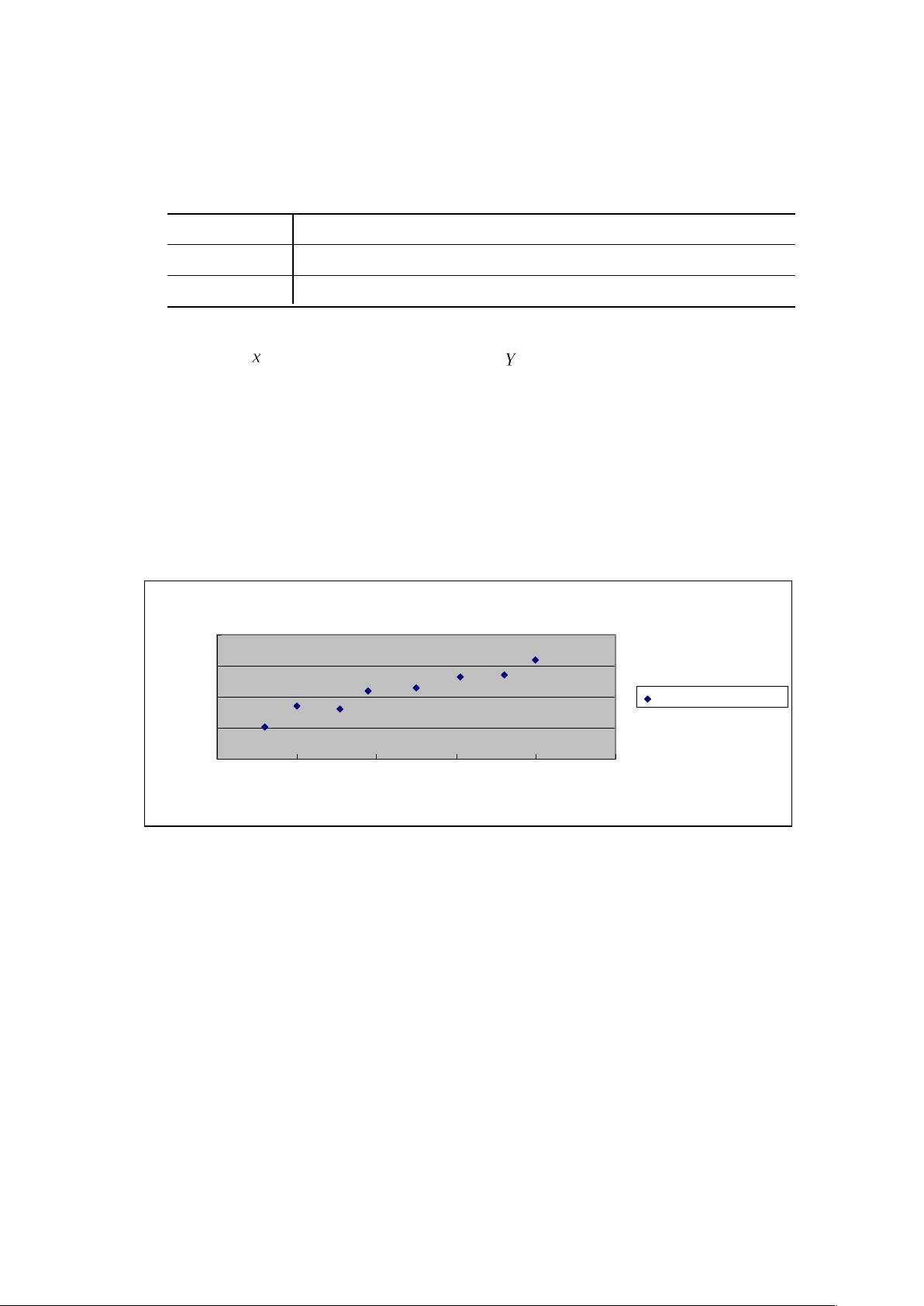
"本文介绍如何使用R软件进行一元线性回归分析，通过具体实例展示了如何构建模型并解释结果。" 一元线性回归是一种统计学方法，用于研究两个变量之间的关系，其中一个变量（自变量）对另一个变量（因变量）的影响。在本例中，产量（X）作为自变量，生产费用（Y）作为因变量，通过建立回归模型来探究两者之间的关联。 在R软件中执行一元线性回归分析的第一步通常是创建散点图。这有助于直观地理解数据分布以及变量间可能存在的关系。在给出的例子中，使用Excel绘制了产量与生产费用的散点图，并在R中使用`plot()`函数重现了这个图。`plot(outputcost$C, outputcost$E)`这行代码将产量（C列）与生产费用（E列）的数据点绘制出来，显示了点大致沿直线分布，表明可能存在线性关系。 接下来，使用`lm()`函数建立线性回归模型。`lm(E~C, data=outputcost)`这一行代码定义了模型公式，其中`E`是因变量，`C`是自变量，`data=outputcost`指定了数据集。运行此命令后，R将计算模型参数。 `summary(lm.sol)`提供了模型的详细统计信息，包括： 1. **系数**（Coefficients）：估计的截距（Intercept）和斜率（C），在本例中截距为46.437，斜率为13.695，它们代表了产量每增加1千吨，生产费用预期会增加13.695万元。 2. **标准误差**（Std. Error）：系数的估计不确定性。 3. **t值**（t value）：系数估计值与其标准误差的比值，用于检验其显著性。 4. **p值**（Pr(>|t|)**：t值对应的概率，若小于显著性水平（通常为0.05），则认为系数显著不为零。 5. **残差标准误差**（Residual standard error）：模型预测值与实际值之间的差异的标准偏差，本例中为9.993万元。 6. **R平方**（R-squared）和调整R平方（Adjusted R-squared）：分别表示模型解释因变量变异性的比例，以及考虑自变量数量后的解释比例。 7. **F统计量**：用于整体模型显著性的检验。 通过这些统计指标，我们可以评估模型的拟合优度、自变量的重要性以及模型是否优于无模型的情况。在本例中，较高的R平方值（0.9292）和显著的t值表明产量对生产费用有显著影响，模型具有较好的解释能力。 R软件提供了一套强大的工具进行一元线性回归分析，从数据可视化到模型建立和结果解读，使得统计建模变得简单易行。通过实例中的步骤，我们可以有效地理解并运用一元回归模型来探索两个变量间的定量关系。