解析树在Python中的应用：构建与遍历

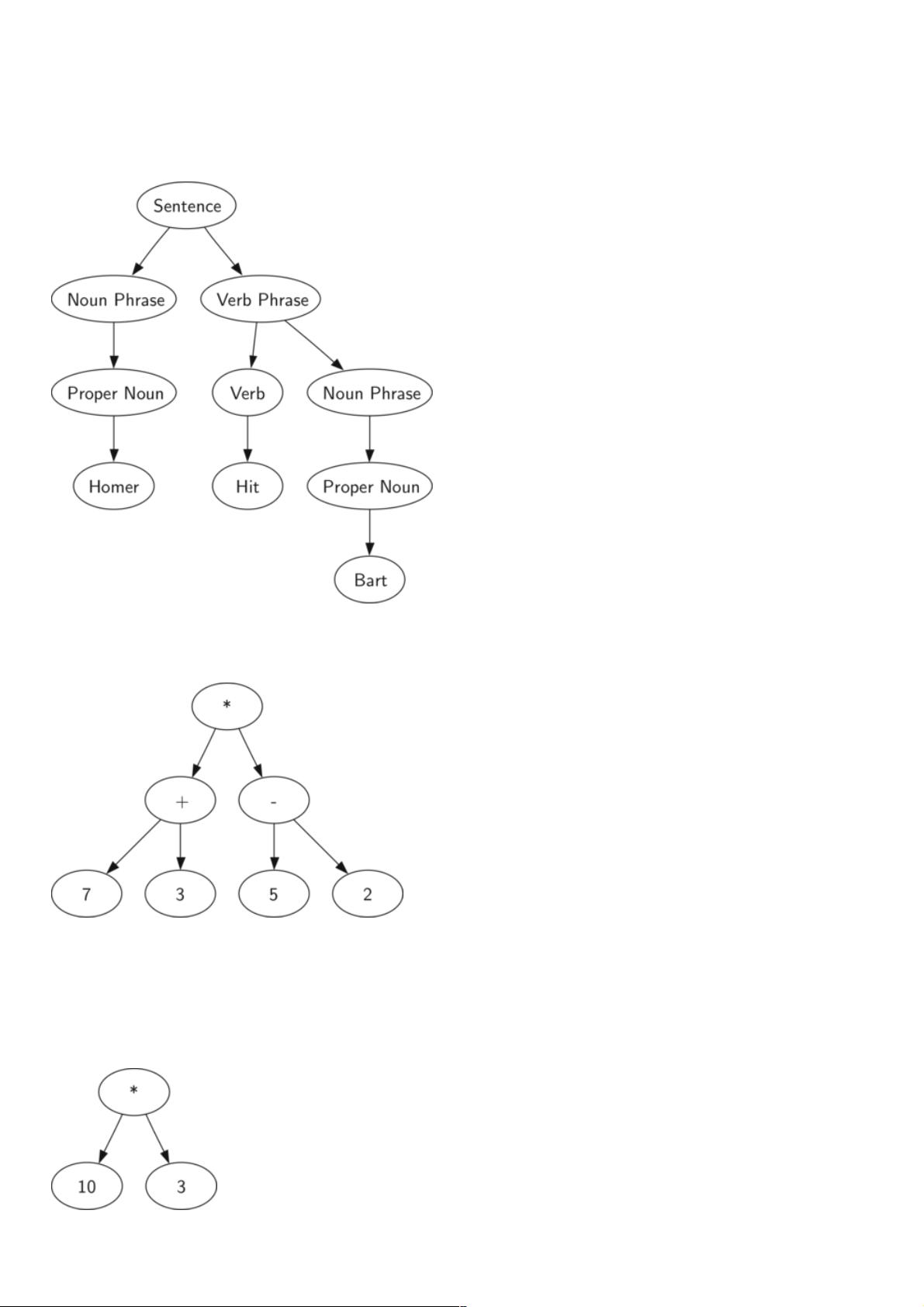
"Python解析树及树的遍历" 解析树是一种数据结构，常用于表示复杂结构，如句子的语法结构或数学表达式的运算顺序。在Python中，解析树可以用来解决实际问题，特别是处理具有层次关系的信息。解析树的每个节点代表一个元素，而子节点则表示该元素的组成部分。例如，在图1中，一个简单句的解析树展示了句子成分的层次结构，使得我们可以逐个处理每个子结构。 图2展示了数学表达式((7+3)*(5−2))的解析树。在这样的树中，乘法运算具有较高优先级，因此我们需要先计算括号内的加法和减法。通过树的结构，我们可以明确运算顺序：首先计算两个子树（加法和减法），然后将子树的结果用于最终的乘法运算。简化后的解析树（图3）更直观地表示了表达式的计算过程。 构建解析树通常涉及以下几个步骤： 1. **分解表达式**：将输入的数学表达式字符串拆分成符号列表，包括操作符、括号和操作数。 2. **构造树结构**：遵循特定的规则，例如： - 当遇到左括号 '(' 时，创建新节点作为当前节点的左子节点，并向下遍历。 - 遇到操作符（如 '+', '-', '/', '*'）时，将该操作符设为当前节点的根值，并创建新节点作为当前节点的右子节点，继续向下遍历。 - 遇到数字时，将该数字设为当前节点的根值，并在完成后返回其父节点。 - 遇到右括号 ')' 时，返回到当前节点的父节点。 在Python中实现这些规则可以构建一个递归算法，递归地处理表达式字符串，构建出对应的解析树。一旦解析树建立完成，我们就可以进行以下操作： - **计算表达式值**：通过遍历解析树，根据运算符的优先级和结合性计算各子树的值，最终得到整个表达式的值。 - **还原表达式**：从解析树中提取信息，生成与原表达式等价的字符串形式。 遍历解析树有三种常见方法：先序遍历、中序遍历和后序遍历。这些遍历方法对于处理树结构的数据至关重要，例如： - **先序遍历**（根-左-右）：先访问根节点，然后递归地遍历左子树，最后遍历右子树。 - **中序遍历**（左-根-右）：先遍历左子树，然后访问根节点，最后遍历右子树。在二叉搜索树中，中序遍历会得到排序后的结果。 - **后序遍历**（左-右-根）：先遍历左子树，然后遍历右子树，最后访问根节点。在计算表达式值时，后序遍历常被用于确保所有子节点的计算在根节点操作之前完成。 掌握解析树及其遍历方法对理解和处理结构化数据至关重要，尤其是在编译原理、自然语言处理和算法设计等领域。在Python中，通过递归和迭代方式实现这些概念，可以灵活地解决各种实际问题。