ADC技术：采样理论与模拟数字转换解析

需积分: 29 29 浏览量更新于2024-07-17 收藏 8.31MB PDF 举报

"该资源是2016年的 Sampling Theory and Analog-to-Digital Conversion 的PDF文档，主要讨论了采样理论以及模拟到数字转换（ADC）的概念和技术。" 在信号处理领域，模拟到数字转换（Analog-to-Digital Converter，简称ADC）是一个至关重要的过程，它将连续的模拟信号转化为离散的数字信号，使得数字系统能够处理这些信号。ADC工作过程中包含了一系列步骤，如采样、量化和编码。采样是ADC的第一步，根据奈奎斯特定理，一个带限信号（Bandlimited Input Signal）可以被无失真地恢复，只要采样频率（fs）至少是信号最高频率成分的两倍，这被称为采样定理。采样过程将连续的时间信号转换成离散的时间序列，即样点，由一系列在时间上等间隔的冲激函数（δ函数）表示。量化是将采样后的样点值映射到离散的数字代码的过程。例如，一个n位ADC能够区分$2^n$个不同的电压级别，每个级别对应一个二进制数字。图中所示的n=4位ADC，其数字输出为2b1b0b，其中每个b代表一位二进制数。零阶保持（Zero-Order Hold, ZOH）电路常用于ADC之后，它保持每个采样时刻的电压值直到下一次采样。ZOH会产生阶跃响应，阶跃的高度等于量化步长（Δ），即相邻量化级间的电压差。量化过程不可避免地引入了误差，称为量化噪声或量化误差。这种误差可能导致信号失真，特别是在低信噪比的情况下更为明显。此外，量化误差也受限于ADC的分辨率，即位数越多，量化误差越小。 ADC的设计和性能评估通常关注以下几个指标：转换速率（每秒转换次数）、分辨率（位数）、线性度、失调和增益误差、噪声和功耗。这些参数决定了ADC在实际应用中的适用性和效率。总结来说，"Sampling Theory and Analog-to-Digital Conversion"主要探讨了采样理论的核心概念，包括采样定理、量化过程和零阶保持在ADC中的作用，以及这些过程对数字信号质量和精度的影响。这本书的缩略版提供了基础的教育理解，但不涉及正式的评审、测试或认证，使用者应根据自身风险进行学习和实践。

Memory Cell

(capacitor)

Electric

Field

Threshold

Level

Stored

Charge

Memory Cell

Contents = 1

Memory Cell

Contents = 0

Compact Disk

Digital Data

Figure 1.9 Memory Cell

Figure 1.10 Compact Disk

A single memory element, as shown in Figure 1.9, holds a stored electric charge. The memory

cell works just like the communications example in Figure 1.8. The content of the memory cell is

determined with a threshold level. The stored amount of charge is above the threshold level, so the

memory cell contains a 1. The combination of quantization and a threshold level creates a reliable

memory device. The compact disk (CD) in Figure 1.10 is another example of 'what is old, is new again.'

The data tracks on the CD are "burnt" with a laser beam. The data tracks on the CD resemble the Morse

code keying waveform in Figure 1.6.

Morse code, digital communications, digital memory, compact disks, and flash memory are all

digital in nature. Even though the technologies appear to be unrelated, the nature of digital technology is

universal. Once data is in digital form, it can be converted from one format to another without any

additional loss of information. The cost of converting information to the digital format is called

quantization error.

15.288

15.292

15.295

15.299

15.303

15.307

15.310

15.314

15.318

15.322

15.235

Gallons of Gasoline

Quantization

$40.65

$40.66

$40.67

$40.68

$40.69

$40.70

$40.71

$40.72

$40.73

$40.74

$40.75

Cost to fill gas tank

Continuous

Range

Discrete Value

15.3

0.3

gallons

15.3 Gallons

$20

25¢

10¢

25¢

$20

5¢

1¢

Total = $40.69

Figure 1.11 Quantization Example (Round Up)

The number of gallons of gasoline is an analog quantity. A one gallon gasoline container can

contain any amount of gasoline from 0 to 1 gallon. The amount of gasoline is a continuous quantity

unlike money or a staircase which are digital.

The gas tank in a hot rod takes 15.3 gallons to fill up. Gasoline costs $2.659 per gallon for a total

of $40.69 (remember the gas station rounds up, e.g. $40.6827 is greater than $40.68 so the cost rounded

up to the nearest penny is $40.69). The exact total is $40.6827. Since money is quantized to the penny,

the gas company will round up the amount to $40.69. The small rounding error is called quantization

error. The quantization error is the cost of working in the digital world. For example, if you spent

$40.74 on gasoline at $2.659 per gallon, the actual amount is somewhere from 15.318 to 15.322 gallons.

The 0.004 gallon range is called quantization error. A second example of quantization error for an image

is shown in Figure 1.12.

Resolution

8 pixels/inch

Resolution

16 pixels/inch

Resolution

50 pixels/inch

Line

Quantization Error

Decreases

(Image Improves)

Digital

Approximations

to Line

Computer

Scanner scans a line

Figure 1.12 Quantization in a Digital Image (Round Down)

As the resolution of the scanner is increased in Figure 1.12, the digital approximation to the line

improves. At the very low resolution of 8 pixels/inch, we can see a definite step effect. At low

resolutions, the line resembles blocks stacked together. Compare Figure 1.12 with the digital nature of

currency in Figure 1.2 and the staircase in Figure 1.3. As the resolution increases, 8, 16, 50

pixels

inch

we see

the digital approximation of the line improves. As the pixel size decreases, the quantization error

decreases, and the image improves. As the image pixel size decreases, more pixels are required for an

image and more memory is required to store a picture.

In a digital camera, quantization occurs due to the size of the image pixels and a second

quantization for the number of possible colors. Quantization due to pixel size and color range are shown

in Figure 1.13. The effects of a limited number of pixels in a digital camera (think 1740 by 1280 pixels)

and the limited number of color shades are shown. The more colors the smoother the transition from

bright to dark. The more colors in an image, the more memory required to store a picture. For example, a

8.5 by 11 inch sheet of paper scanned in at a resolution of 100 pixels per inch with 256 shades of red,

blue, and green will require 2.7 megabytes (

mega 2 1,048,576

) of storage.

In a digital camera, or scanner, the

colors in the image are also quantized

Quantization due to fixed number of shades of blue

Continuous Blue Color Range Quantized Blue Color Range

Input Image

Digital Camera

Output is Quantized

Amplitude QuantizationImage Pixel Size Quantization

Quantization due to finite pixel size

Figure 1.13 Pixel Quantization and Color Quantization in Images

1.3 Pulse Code Modulation

Audio

PCM

Waveform

PCM plus noise

Threshold

recovered

PCM waveform

Audio

PCM Waveform

Time (sec)

Voltage

Serial Data Stream

-2

-1

0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1

Threshold Recovered PCM Waveform

Time (sec)

Voltage

Serial Data Stream

-2

-1

.1 .2 .3 .4 .5 .6 .7 .8 .9 10

PCM Waveform plus Noise

Time (sec)

Voltage

PCM Waveform plus Noise

-2

-1

0 .1 .2 .3 .4 .5 .6 .7 .8 .9 1

Threshold Level

Figure 1.14 Simplified Telephone System

A simplified telephone network, not quite circa Alexander Graham Bell, is shown in Figure 1.14.

Please do not call the phone company and ask the operator to explain pulse code modulation. As pointed

out in sections 1.1 and 1.2, a digital communications signal can be recovered with a simple threshold

level.

In a telephone network, audio is converted to a series of pulses. The pulse waveform in

Figure 1.14 is called pulse code modulation (PCM). In [1.4], Shannon proves a noisy PCM waveform

can be regenerated after transmission with an arbitrarily small number of errors. For a small amount of

noise [1.6], the noisy PCM waveform in Figure 1.14 can be regenerated resulting in a clean digital

waveform (bottom graph). With PCM, the quality of the telephone audio is not dependent of the length

of the telephone line, no matter how far the telephones are apart (thousands of miles). The benefits of

PCM are a high quality telephone connection and the cost of the technology is quantization error

introduced in section 1.2.

PCM was patented by A. Reeves in 1938 in France, 1939 in Britain, and 1942 [1.7] in the United

States. A secure PCM communications system, used by Churchill and Roosevelt, called SIGSALY, was

developed by Reeves in 1943 [1.8]. A more modern PCM telephone system was patented by Oliver, et al.

[1.9] in 1957. Digital technology has been in use for decades now and remember the telegraph goes back

to 1840!

The next section introduces Shannon's sampling theorem [1.3], [1.10]. The sampling theorem

provides the conditions for converting analog (continuous) to discrete (digital is an approximation to

discrete), and back to analog.

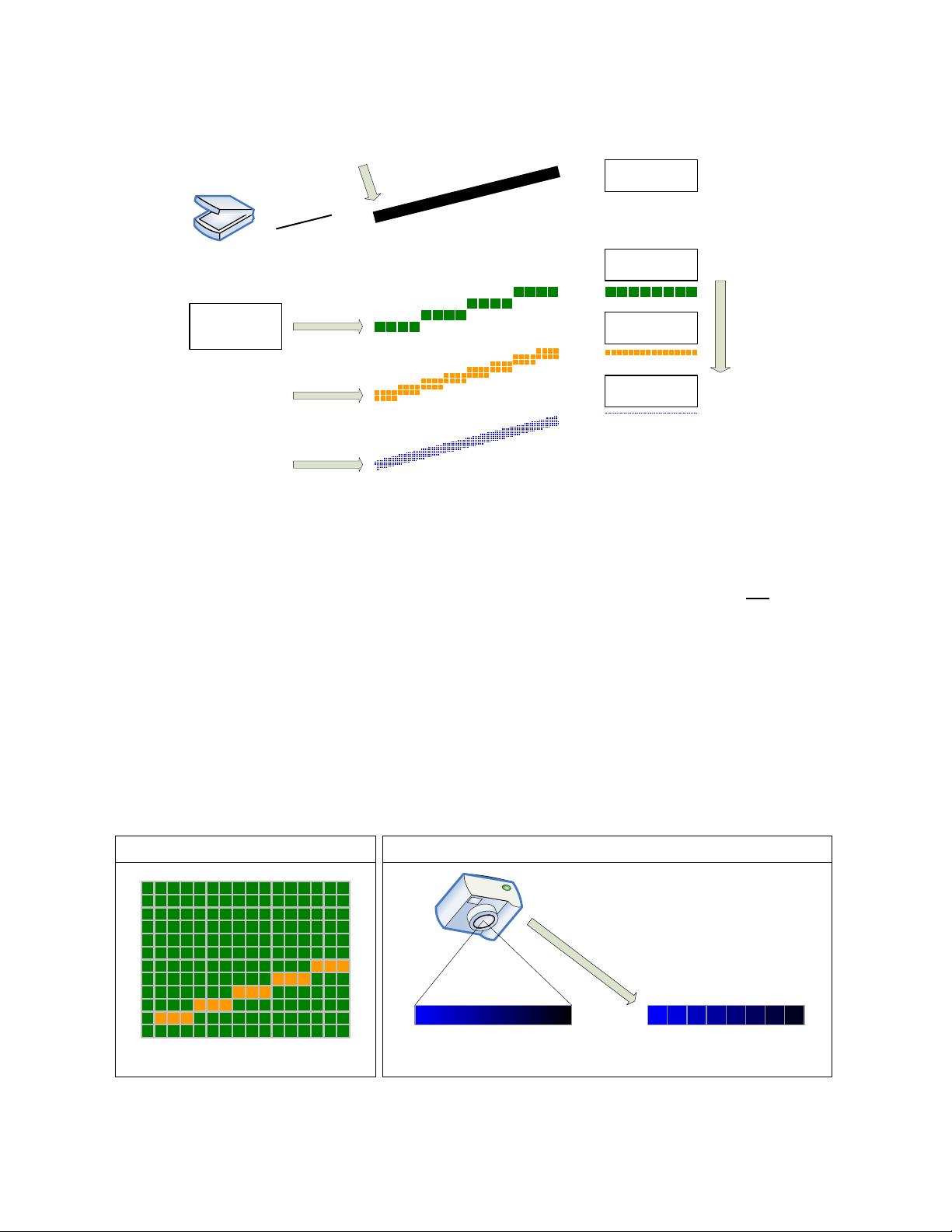
Filter

Sample

Interpolation

Filter

Microphone

Speaker

Figure 1.17 Sampling Theory Example

A simple application of Shannon's sampling theorem is shown in Figure 1.17. The input audio

analog signal from the microphone is low-pass filtered. Sampling the output of the low pass filter results

in a discrete time signal (digital is an approximation of discrete time). An interpolation filter connects the

sample points together forming a smooth curve. Chapters 2 and 3 introduce the tools required to prove

Shannon's sampling theorem. Chapter 4 presents a simple graphical derivation of Shannon's sampling

theorem. A formal mathematical proof of Shannon's sampling theorem is also covered in Chapter 4.

Appendix A summarizes the proof of Shannon's sampling theorem.

1.5 Chapter Summary

Chapter 1 introduces the digital world by pointing out that money is digital. Several digital

technologies are introduced: Morse code, computer memory, compact disks, and pulse code modulation.

Even though the technologies appear unrelated, the digital format is universal. Once data is in a digital

format, it can be easily converted to any other digital format without loss of information (excluding lossy

data compression). When an analog quantity (gallons of gasoline at $2.659 per gallon) is converted to

digital (think money), rounding off to the nearest penny results in quantization error. If you are thinking

about capitalizing off of the round-off error; don't, it has already been tried before in "Superman II"

[1.12]. Quantization error is the cost for the benefit of reliable storage of digital information.

Shannon's sampling theorem provides the conditions for reconstructing the original signal from

sample values. The sinc( ) interpolation function connects the sample values together forming a smooth

curve reconstructing the original signal.

Terms introduced in Chapter 1 include: analog, digital, discrete, continuous, quantization,

quantization error, rectangular window, sinc( ) function, Shannon's sampling theorem, coding, pulse

code modulation, interpolation and regeneration.

1.6 Book Organization

A simple introduction to sampling theory, and analog-to-digital conversion is presented in

Chapter 1. To understand the mathematics of Shannon's sampling theorem, a background in linear

systems and Fourier analysis is required. An introduction to linear systems is presented in Chapter 2.

The mathematical tools for working with linear systems are covered in Chapter 3. For those unfamiliar

with linear systems, a simple understanding of what a low pass filter is, will be sufficient to understand

the key concept of Shannon's sampling theorem. A graphical derivation of Shannon's sampling theory is

found in Chapter 4. A complete proof of Shannon's sampling theorem is found at the end of the chapter.

An easy to understand explanation of the binary number system and how it applies to analog-to-digital

converters is covered in Chapter 5. A useful part of Chapter 5 is how to solve the problem of a signed

10 bit analog-to-digital converter connected to a 16 bit microprocessor (or a signed

bit analog-to-

digital converter connected to a n bit processor). Chapter 6 focuses on quantization, quantization error

and coding. Flash, pipeline, successive approximation, and delta sigma (ΔΣ) analog-to-digital converter

technologies are described in Chapter 7. Performance metrics and testing of analog-to-digital converters

剩余203页未读，继续阅读

qq_18381045

粉丝: 14
资源: 58

ADC技术：采样理论与模拟数字转换解析

TMS320x2802x, 2803x Piccolo Analog-to-Digital Converter (ADC) and Comparator.pdf

2019 Analog-and-Algorithm-Assisted Ultra-low Power Biosignal Acquisition Systems

Analog Devices 模数转换系列AD芯片ALIUTM原理图库PCB库（AD集成库）2404个.zip

stm32 adc128s102

stm32l476RG ADC

Statistical knowledge outline

A-D转换的过程不包括

stm32 ad7606

ad4680 verilog

TIM+ADC+DMA

最新资源