信号与系统复习：傅立叶变换与系统响应解析

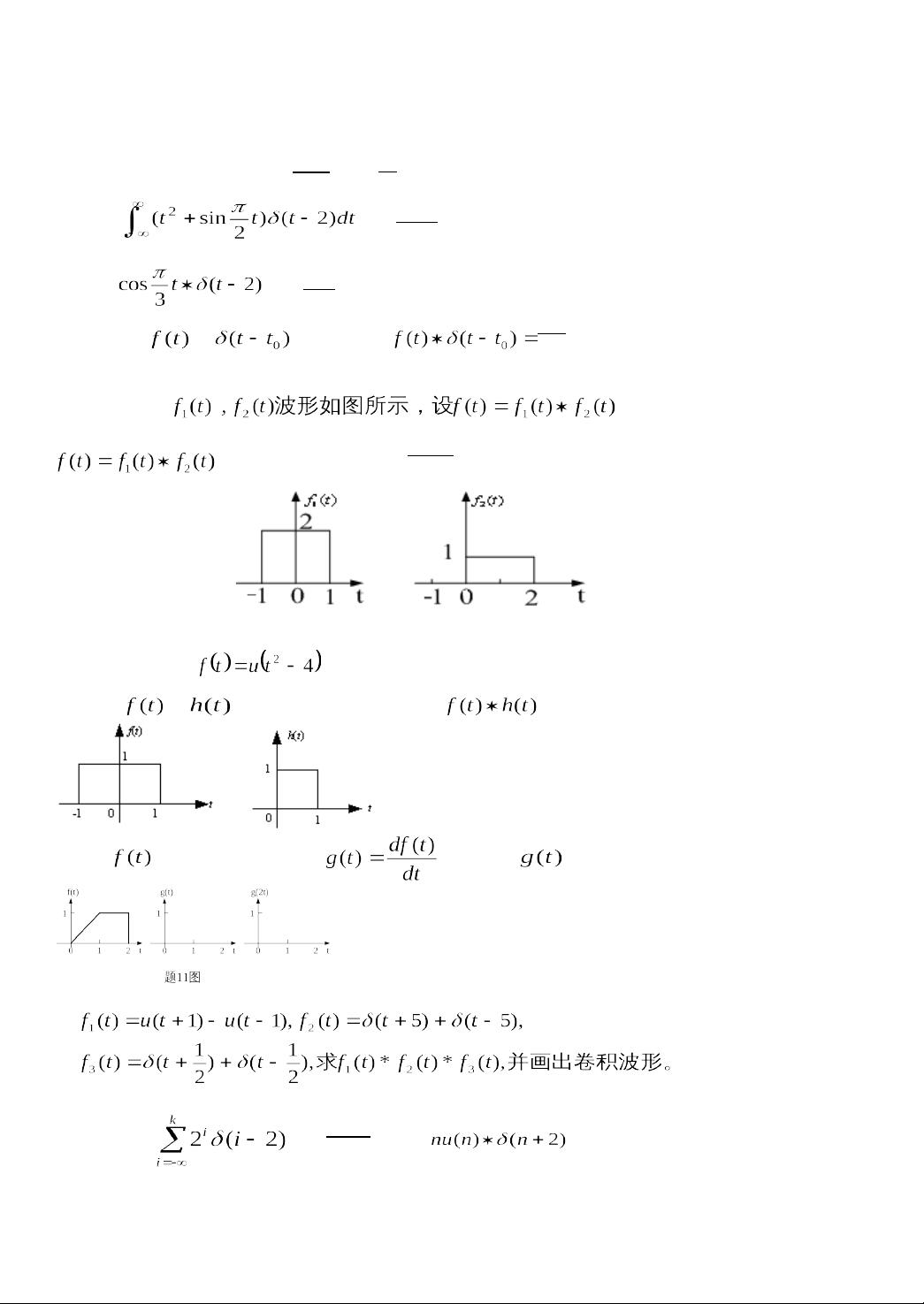
"这篇资料是关于信号与系统课程的复习要点，涵盖了信号的基本变换、傅立叶级数、傅立叶变换以及拉普拉斯和Z变换等核心概念，并通过具体的卷积计算、连续时间系统响应的分析以及傅立叶变换性质的应用进行了深入探讨。" 在信号与系统的学习中，有几个关键的知识点需要掌握： 1. **基本信号**：包括冲激函数δ(t)和阶跃函数u(t)，它们是分析系统的重要工具。冲激函数在卷积运算中起到关键作用，例如题目中的x(k+3)*δ(k-2)的卷积结果为x(k+1)。 2. **傅立叶级数**：用于将周期性信号分解为正弦和余弦函数的和，理解和记忆欧拉公式是关键，它简化了sin和cos的表示。 3. **连续时间函数的傅立叶变换**：用于分析非周期信号，需掌握基本变换公式和一些常见信号的变换性质，如线性和时域卷积。 4. **离散时间函数的傅立叶变换**：与连续时间的傅立叶变换类似，但应用于离散信号，同样需要理解变换性质。 5. **拉普拉斯变换**：适用于连续时间系统的分析，比傅立叶变换有更广泛的适用范围，理解系统的稳定性和因果性是关键。 6. **Z变换**：对应于离散时间系统的分析，比离散傅立叶变换更广泛，同样需要考虑系统的稳定性和因果性。 在卷积计算部分，题目提供了几个实例，如积分计算和特定信号的卷积。例如，题目中给出的连续信号卷积，以及序列的卷积和。卷积运算是理解系统行为的关键，因为它描述了输入信号如何通过系统被处理。 连续时间系统的响应分析涉及线性时不变（LTI）系统，包括零状态响应（ZSR）和零输入响应（ZIR）。例如，通过输入和输出波形可以推断出系统的响应，或者通过系统微分方程来求解。 在傅立叶变换及其性质方面，我们需要计算信号的傅立叶变换，理解其频域表示，并能确定周期信号的Fourier级数系数。 通过以上知识点的复习和练习，学生可以深入理解信号与系统的理论，并能运用到实际问题中去解决信号处理和系统分析的问题。对于电路系统，可以通过冲激响应和阶跃响应来研究其动态特性。在傅立叶变换的运用中，了解其性质对于信号的频谱分析至关重要。