GPU上的基于分析解的轮廓卷积曲面建模
188 浏览量
更新于2024-08-28
收藏 1022KB PDF 举报
"这篇论文提出了一种在GPU上基于草图的卷积曲面建模的分析解决方案，特别关注于有限支持和无限支持核函数的平面多边形骨架。通过应用格林定理，将对平面多边形的双重积分转换为沿着多边形轮廓的简单积分，降低了计算成本，并实现了GPU上的高效并行计算。对于有限支持的核函数，还提出了一种骨架裁剪算法来计算有效骨架。这些分析解决方案被集成到一个GPU原型建模系统中，该系统支持点、多边形线和平面多边形骨架。可以交互式地轻松建模任意 genus 的复杂对象。"
本文的核心知识点包括：
1. **卷积表面**：卷积表面是一种用于建模具有复杂拓扑变化的对象的方法，因为它能够平滑地适应形状的变化。
2. **闭合形式解**：论文提出了闭合形式的卷积解决方案，这意味着可以直接求得精确的数学表达式，而无需迭代或其他数值方法。
3. **平面多边形骨架**：骨架是形状的基本结构，论文专注于平面多边形骨架，它们在建模过程中提供了一种有效的表示方式。
4. **格林定理**：格林定理是微积分中的一个重要工具，它在这篇文章中被用来将对平面多边形的双重积分转化为对多边形轮廓的单次积分，从而简化了计算过程并提高了效率。
5. **GPU并行计算**：通过利用GPU的强大并行处理能力，可以加速计算密集型的卷积过程，提高建模速度。
6. **有限支持与无限支持核函数**：核函数是卷积过程中的关键元素，有限支持核仅在一定范围内影响形状，而无限支持核在整个域内都有影响。文章提供了两种情况下的解决方案。
7. **骨架裁剪算法**：对于有限支持的核函数，需要确定有效的骨架部分。骨架裁剪算法用于识别和计算这部分骨架。
8. **GPU原型建模系统**：这些分析解决方案被集成到一个GPU驱动的系统中，该系统允许用户交互式地创建和编辑模型。
9. **点、多边形线和平面多边形骨架的支持**：该建模系统不仅支持基本的点和线骨架，还支持更复杂的平面多边形骨架，增强了建模的灵活性和多样性。
10. **任意 genus 的复杂对象建模**：系统能够建模具有任意拓扑复杂性的对象，如多孔或有洞的形状，这对于3D建模和设计来说是非常有价值的特性。
这篇论文提出的分析解决方案为实时、交互式的复杂3D建模提供了一种有效且高效的工具，特别是在处理具有动态拓扑变化的对象时。通过结合GPU的并行计算能力，它显著提升了建模的效率和精度。
Analytical solutions for sketch-based convolution surface modeling on the GPU 1117
used in the sketch-based ShapeShop [23, 24] system. As a
skeleton-based modeling tool [5], convolution surfaces were
naturally introduced into sketch-based modeling [27]. The
sketch-based system in [1] extracts the point skeletons of the
sketched outlines, and then utilizes spherical implicit func-
tions to construct the blobby 3D models. In order to model
complex objects such as cylindrical and planar surfaces, too
many point-skeletons are needed to avoid bumps. Cylindri-
cal surfaces can be easily modeled using line skeletons [2,
4, 27], as convolution solutions for line skeletons can be ob-
tained analytically [12–14, 26]. The triangle skeletons are
also adopted by the system in [2] to construct the palm com-
ponent of a hand model where an extracted polygon has to
be triangulated in order to allow for the evaluation of its field
values.
3 Field value calculation for planar polygon skeletons
In this section, after giving a brief introduction to convolu-
tion surfaces, we deduce analytical solutions for planar poly-
gon skeletons with different kernels using a curve integral
method. Our approach allows us to efficiently evaluate the
field value at any point analytically.
3.1 Convolution surfaces
A convolution surface is an iso-surface defined in an im-
plicit scalar field whose values are evaluated by accumulat-
ing contributions from 3D points of a skeleton. The con-
tribution usually decreases rapidly when the distance be-
tween a point in space and a skeleton is increased. Here, we
adopt the convolution surface definition by McCormack and
Sherstyuk [22]. Let p(x,y,z) be a space point in
3
, and
g :
3
→be a geometric function representing a model-
ing skeleton V :
g(p) =
1, p ∈ skeleton V
0, otherwise
. (1)
Let f :
3
→be a potential function which defines the
field with a single point in the skeleton V , and let q be
a point in V . Then the total field value contributed by the
skeleton at point p is the convolution of functions f and g:
F(p) =
V
g(q)f (p −q)dV =(f ⊗g)(p). (2)
f is also called the convolution kernel function. Theoret-
ically, any geometric primitive can be used as a skeleton.
However, closed-form solutions depend on both the kernel
and the skeleton.
3.2 Curve integral for planar polygon skeletons
Let K(v
0
v
1
v
2
···v
n
v
0
) be a planar polygon skeleton, the
field value at a point p for this skeleton is computed by a
double integral according to (2). For a kernel function with
infinite support, the integration is evaluated on the entire
polygon. However, for a finite support kernel function, the
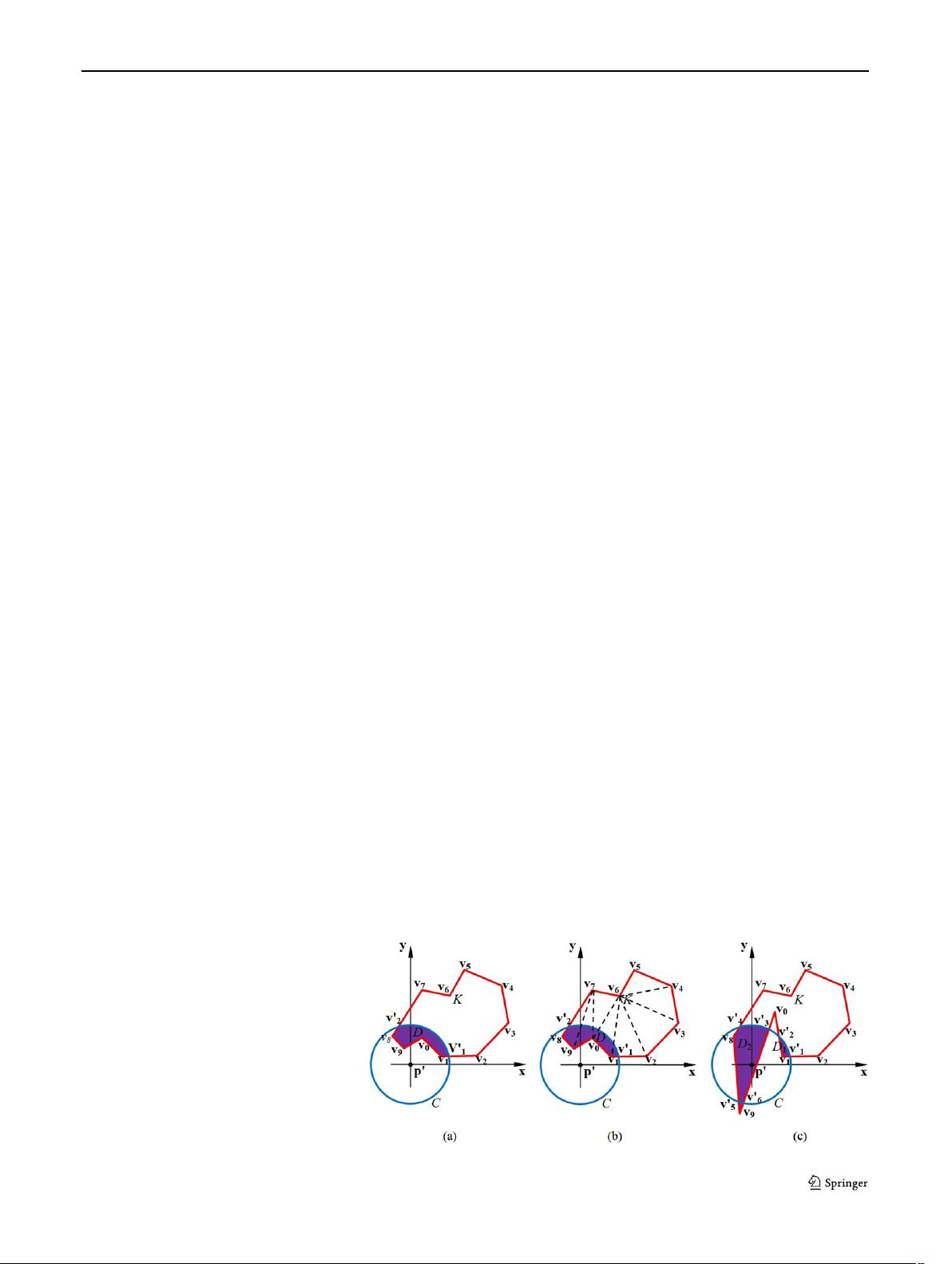
valid skeletons are areas in the clipping sphere centered at
p, as shown in Fig. 1(a). Generally, the intersecting area is a
polygon or multiple polygons whose boundaries consist of
arcs and line segments. It is difficult to perform the integra-
tion on the intersecting area directly. One solution is to de-
compose the polygon into triangle segments and chord seg-
ments, and then evaluate the convolution integral for each
type [15], as shown in Fig. 1(b). However, such a solution is
not suitable for GPU implementation because GPU branch-
ing is usually slow. Here, we present a closed-form solution
by converting the double integral into a curve integral using
Green’s theorem. As the integral computation can be per-
formed for each edge one by one, we can make better use of
the GPU’s enormous floating point computing capacity.
The field value at point p for a planar polygon skeleton
can be computed directly without the polygon triangulation.
With the integration domain D and its boundary l, the field
value at point p is:
F(p) =
D
f(r)dxdy, (3)
where r =p −q denotes the Euclidean distance between
points p and q, q ∈D. This double integral can be computed
Fig. 1 The regions for the
convolution integral. The valid
polygon skeleton for finite
support kernels is shadowed
in (a). Illustration in (b)
triangulates the polygon before
using closed-form convolution
surface solutions for triangle
skeletons. (c) shows our
clipping between a general
polygon and the clipping sphere
剩余10页未读，继续阅读
2020-01-07 上传
2021-02-21 上传
2021-02-12 上传
2021-02-10 上传
2019-08-13 上传
2021-02-04 上传
2020-02-29 上传
2021-06-26 上传
2021-03-08 上传
weixin_38748875
- 粉丝: 10
- 资源: 951
我的内容管理
展开
最新资源
- 构建基于Django和Stripe的SaaS应用教程
- Symfony2框架打造的RESTful问答系统icare-server
- 蓝桥杯Python试题解析与答案题库
- Go语言实现NWA到WAV文件格式转换工具
- 基于Django的医患管理系统应用
- Jenkins工作流插件开发指南：支持Workflow Python模块
- Java红酒网站项目源码解析与系统开源介绍
- Underworld Exporter资产定义文件详解
- Java版Crash Bandicoot资源库：逆向工程与源码分享
- Spring Boot Starter 自动IP计数功能实现指南
- 我的世界牛顿物理学模组深入解析
- STM32单片机工程创建详解与模板应用
- GDG堪萨斯城代码实验室：离子与火力基地示例应用
- Android Capstone项目：实现Potlatch服务器与OAuth2.0认证
- Cbit类：简化计算封装与异步任务处理
- Java8兼容的FullContact API Java客户端库介绍
