Abstract—In this paper an optimal control method for parafoil
system homing planning is introduced, which includes
multi-phase homing arrangement, optimal homing path
calculation using genetic algorithm(GA), and Bezier curves
based path planning for parafoil terminal guidance to deal
with the situation of variable glide ratios. L1 nonlinear
algorithm is adopted to make trajectory tracking. Comparison
simulations results show that L1 tracking algorithm has more
rapid response speed, higher precision and better wind
resistance than PD tracking algorithm in homing path
planning with different initial positions and with or without
wind.
I. INTRODUCTION
Comparing with ordinary parachute, Parafoils have good
stability, excellent gliding performance, and maneuverability.
All these characteristics make it more and more popular in the
area of spacecraft recovery and remote control of the
precision airdrop parafoils, and it has become the focus
research of recovery technology [1].
Homing control of the parafoil system is very important in
the entire flight. In the early engineering applications, radial
homing method are generally adopted as homing control
strategies [2,3]. After 1970s, optimal control based homing
theory is developed, and Multi-phase homing control method
[1,4,5,6] is used in practical application, which simplifies the
whole process of control and make homing planning more
robust and easier.
Multi-phase homing strategy segments the entire homing
path according to different stages and characteristics of
homing process. So the parafoil homing process is divided
into three stages which are called “radial flight” “hover cutting
high” and “headwind-landing”. According to the requirements
of the parafoil system landing, parameters of each stage will
be optimized. Soppa [4], Sim [5], Jann [6] and Hogue [7] and
other scholars have studied the multi-phase homing method
using different strategies. These strategies have described
how to return to the base station with multi-phase, but the
paths are easy enough to meet every situation. Xiong Jing [1]
*Resrach supported by National Natural Science Foundation of China
(Grand No. 61528303 and 61503369).
Liying Yang is Master candidate of State Key Laboratory of Robotics,
Shenyang Institute of Automation, Shenyang, 110168, China (e-mail:
yangliying@sia.cn).
Xiaoguang Zhao is with the College Of Information Science and
Engineering, Northeastern University, Shenyang 110819, China (e-mail:
zhaoxiaoguang@sia.cn).
Feng Gu is with the State Key Laboratory of Robotics, Shenyang Institute
of Automation, CAS, Shenyang 110016, China (e-mail: gufeng@sia.cn).
Yuqing He is with the State Key Laboratory of Robotics, Shenyang
Institute of Automation, CAS, Shenyang 110016, China (e-mail:
heyuqingn@sia.cn). corresponding author
developed a novel method of multi-phase homing in which
GA is used for path planning, however, in the whole homing
process, the glide ratio is fixed and only one plan being
operated.
Multi-phase homing is the key problem of the accurate
landing of parafoil system. In this paper, a complete solution
of parafoil system homing are designed. Trajectory
optimization can be transformed into parameter optimization
so that we can use GA to solve the problem. In the air,
parafoil may be subject to a variety of disturbances, which
will cause the change of glide ratio, and parafoil cannot reach
the target point while following the path of previous planning.
Thus Bezier curves are used for re-planning in upwind
landing segment. Then L1 tracking algorithm can be used to
track the planning path and reach the target point. In this
paper, firstly, the multi-phase homing of parafoil system with
fixed glide ratio. Secondly, multi-phase homing with
non-fixed glide ratio is described. Thirdly, L1 tracking
algorithm with trajectory tracking is studied, in which its
advantages in the condition with wind is shown.
II. MULTI-PHASE HOMING OF PARAFOIL SYSTEM WITH FIXED
GLIDE RATIO
A. Description of Multi-phase homing
The parafoil homing process is divided into threee stages
which are called “radial flight” “hover Cutting high” and
“headwind-landing”. Parafoil uses different control methods
in different stages to improve the accuracy of homing and
enhance the safety of landing.
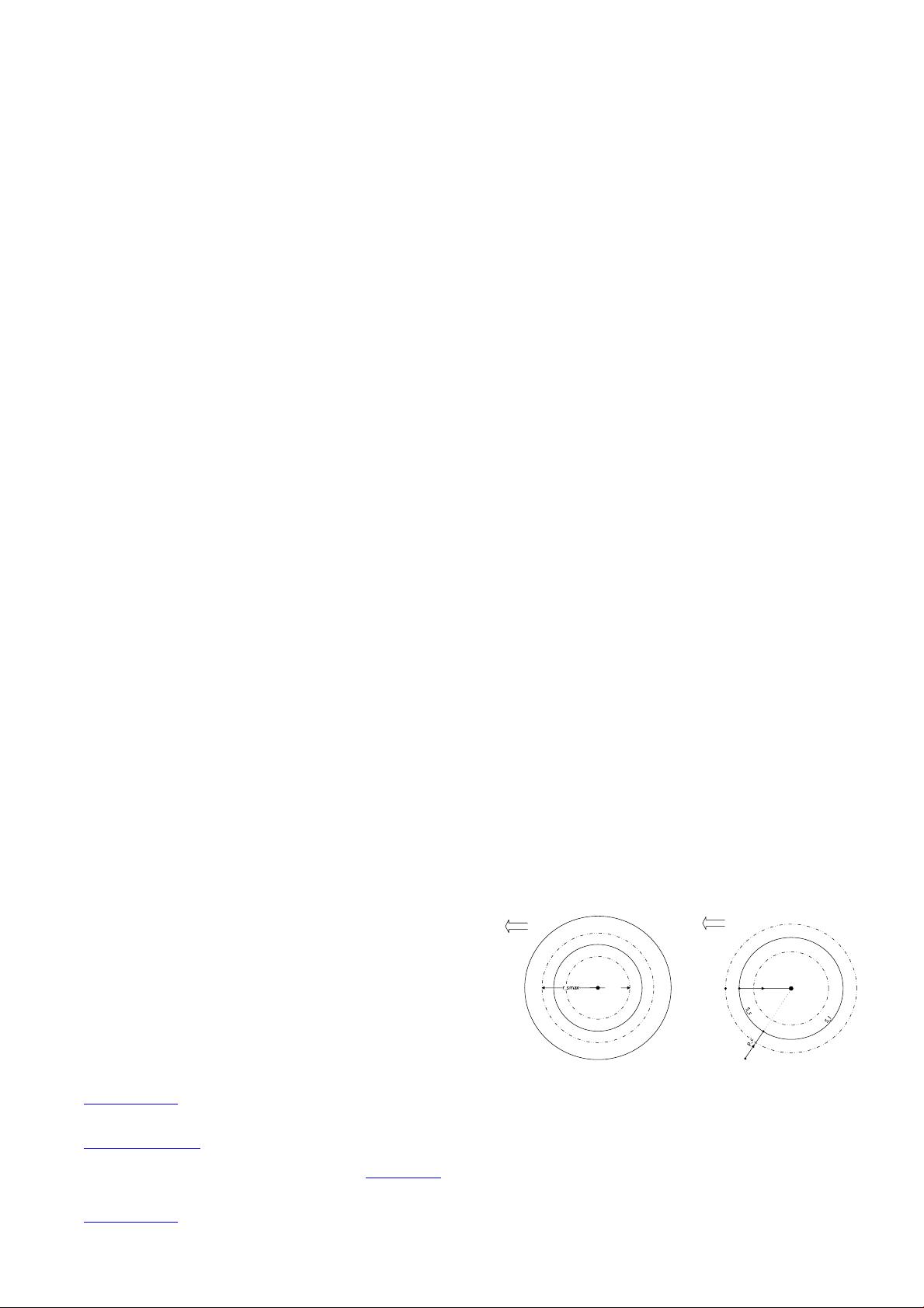
Classic Multi-phase homing principle is shown in Figure
1.