C语言实现图的存储与操作:遍历、最小生成树、最短路径
需积分: 9 170 浏览量
更新于2024-07-15
收藏 224KB DOCX 举报
"该文档是关于图的表示实现与应用的实验指导,涵盖了图的静态存储、遍历算法以及最小生成树、最短路径和关键路径的计算方法。实验使用C语言在Visual Studio 2010环境下进行,要求学生理解和实现相关算法,并通过实验报告的形式提交成果。"
在计算机科学中,图是一种重要的数据结构,用于表示对象之间的关系。这个实验主要关注图的表示和其在C语言中的实现。图可以使用邻接矩阵或邻接表两种方式来存储。
1. **邻接矩阵**:对于无向图,邻接矩阵是一个二维数组,其中`graph[i][j] = 1`表示顶点i和顶点j之间存在边,否则为0。对于有向图,邻接矩阵是对称的,如果`graph[i][j] = 1`,则表示存在从顶点i到顶点j的有向边。
2. **邻接表**:邻接表由一个数组和多个链表组成,数组对应图中的每个顶点,链表存储与其相邻的所有顶点。这种方式节省空间,特别是当图稀疏时。
实验内容涉及以下算法:
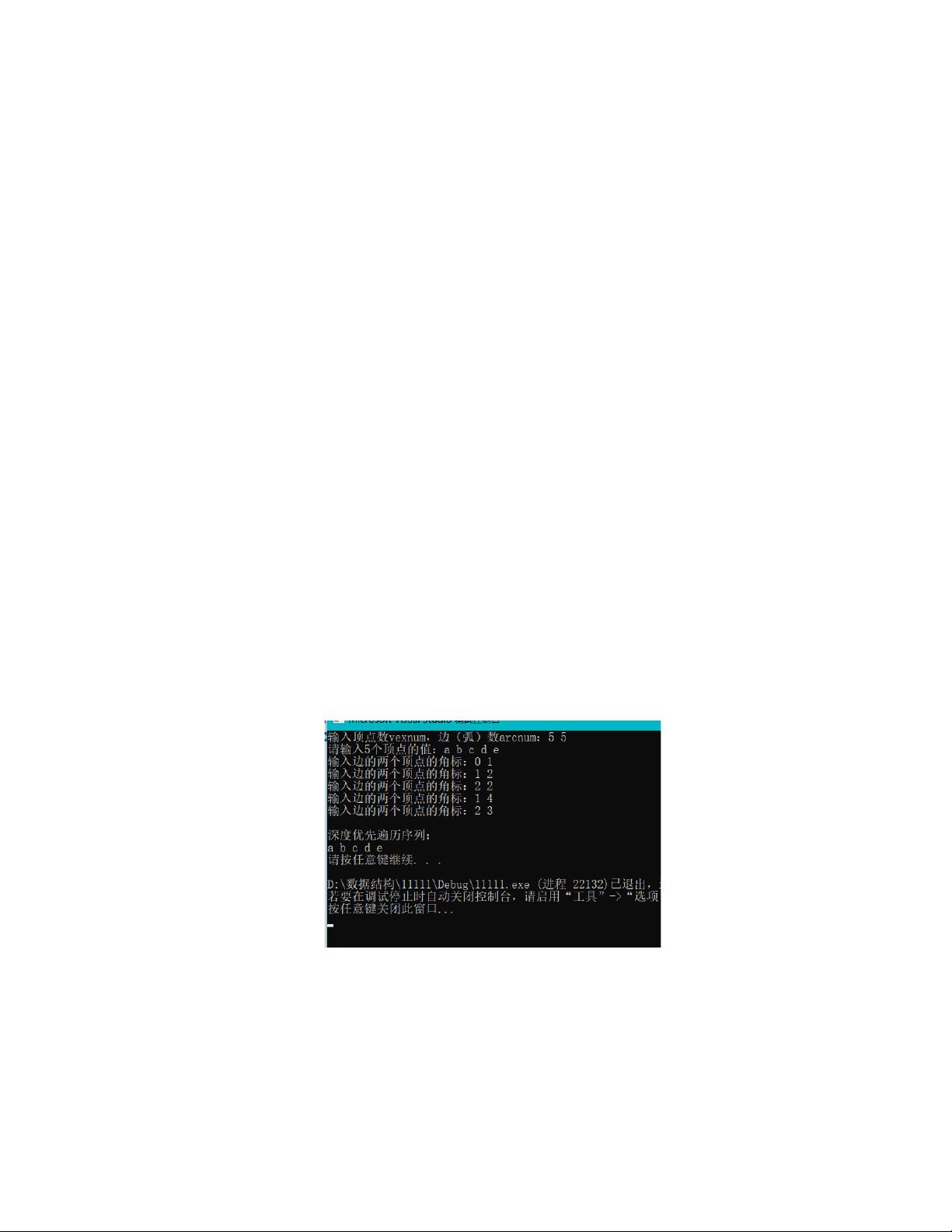
- **深度优先遍历(DFS)**:从一个顶点开始,递归地访问所有与其相连的顶点,然后再访问这些顶点的邻居,直到遍历整个图。DFS可以使用递归或栈来实现。
- **广度优先遍历(BFS)**:从源顶点开始,按层次顺序访问所有顶点。使用队列来保持待访问的顶点。
- **最小生成树**:如普利姆(Prim)和克鲁斯卡尔(Kruskal)算法,用于寻找图中连接所有顶点的最小权重边集,形成一棵树。
- **普利姆算法**:从任意一个顶点开始,每次添加一条与已选择边连接且权重最小的边,直到所有顶点都包含在内。
- **克鲁斯卡尔算法**:首先将所有边按权重升序排序,然后依次添加未形成环的边。
- **最短路径**:Dijkstra算法用于找到单源最短路径,而Floyd算法则计算所有顶点对之间的最短路径。
- **Dijkstra算法**:从源节点开始,每次扩展当前最短路径的下一个顶点,直到到达目标节点。
- **Floyd算法**:使用动态规划,逐步更新所有顶点对的最短路径。
- **拓扑排序**:对于有向无环图(DAG),拓扑排序给出一个没有环的顶点线性顺序。
- **关键路径**:在有向加权图(AOE网)中,关键路径是项目进度管理中的重要概念,它给出了完成项目所需的最短时间,即最长的活动序列。
实验要求学生熟悉并实现上述算法,通过编程练习来加深理解,并提交实验报告,包括代码、运行结果和分析。实验环境为Windows系统下的Visual Studio 2010,提供了充足的硬件和软件支持。实验预备工作强调了预习和实践操作的重要性,确保学生在实验前对相关知识有充分了解。
2020-12-20 上传
我想学会编程kk
- 粉丝: 1
- 资源: 16
最新资源
- RoslynQuoter:Roslyn工具,用于给定的C#程序显示语法树API调用以构造其语法树
- 奢华酒店别墅预定响应式模板
- 西蒙游戏
- 交通灯控制PLC程序.rar
- 电信设备-基于邻域信息与高斯滤波的CBCT全景图非线性锐化增强方法.zip
- invisiblecities:书本探索
- 华硕TUF B450M-PLUS GAMING驱动程序下载
- 教育门户手机网站模板
- anonym-blog:博客系统
- 零基础也能学会的目标检测:YOLO入门指南!.zip
- 韩国平网程序.rar
- rlisp:用Ruby编写的简单方案解释器
- masstech-info-demo-page
- template-react-styled-components:模板criado做零通信创建应用程序的应用程序样式化组件
- starting-websockets:Makers Academy 第 7 周活动 - Websockets 和 Socket.io 简介
- GUI Timestack processing software-开源