二叉排序树查找详解与C++实现

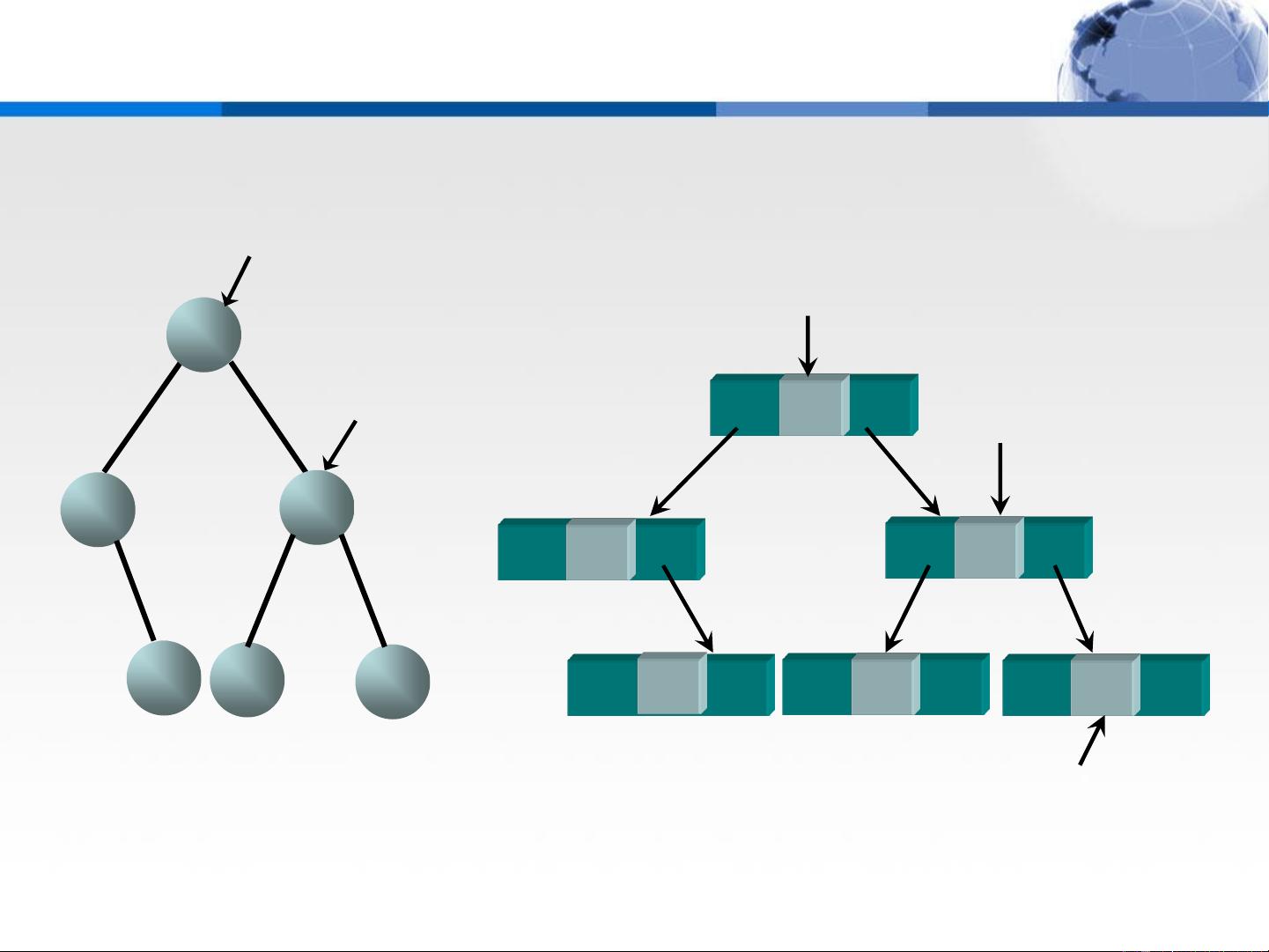
本章节主要探讨了数据结构中的树表查找技术，特别是关注二叉排序树（Binary Search Tree，BST）这一核心概念。二叉排序树是一种特殊的二叉树，它满足以下特性： 1. 如果一个节点的左子树不为空，那么左子树中的所有节点的值都小于该节点的值。 2. 如果一个节点的右子树不为空，那么右子树中的所有节点的值都大于该节点的值。 3. 二叉排序树的每个子树自身也是一个二叉排序树。 在实现上，二叉排序树通常以递归的方式来定义。其存储结构是基于二叉链表，通过类`BiSortTree`进行操作，类中包含如下的关键成员和函数： - `BiSortTree(int a[], int n)`：构造函数，用于初始化二叉排序树，传入一个整型数组和数组长度。 - `~BiSortTree()`：析构函数，用于在对象生命周期结束时清理资源。 - `InsertBST(BiNode<int> *root, BiNode<int> *s)`：插入操作，将新的结点`s`插入到二叉排序树中，根据节点值的大小关系决定插入的位置，递归调用直到找到合适的位置。 - `DeleteBST(BiNode<int> *p, BiNode<int> *f)`：删除操作，用于在已存在的二叉排序树中移除指定节点，涉及搜索和调整节点结构。 - `SearchBST(BiNode<int> *root, int k)`：查找操作，接收根节点和键值`k`，在树中查找是否存在对应的节点。 当二叉排序树以链表形式存储时，中序遍历会返回一个按关键字有序的序列。例如，给定一个二叉排序树，当插入值为98的新节点时，树的结构会相应更新，保持排序性。通过这些函数，可以有效地在二叉排序树中执行查找、插入和删除等操作，提高了数据的查找效率，因为搜索过程的时间复杂度在平均情况下为O(log n)。 理解并熟练掌握二叉排序树的这些核心概念和操作对于学习数据结构和算法至关重要，它们在许多实际应用中，如数据库索引、文件系统和编译器等，都有广泛的应用。在编程实践中，实现这些功能可以使用C++等面向对象语言，通过递归和迭代的方式灵活地处理树的节点关系。