离散傅立叶变换详解：从周期序列到频域抽样

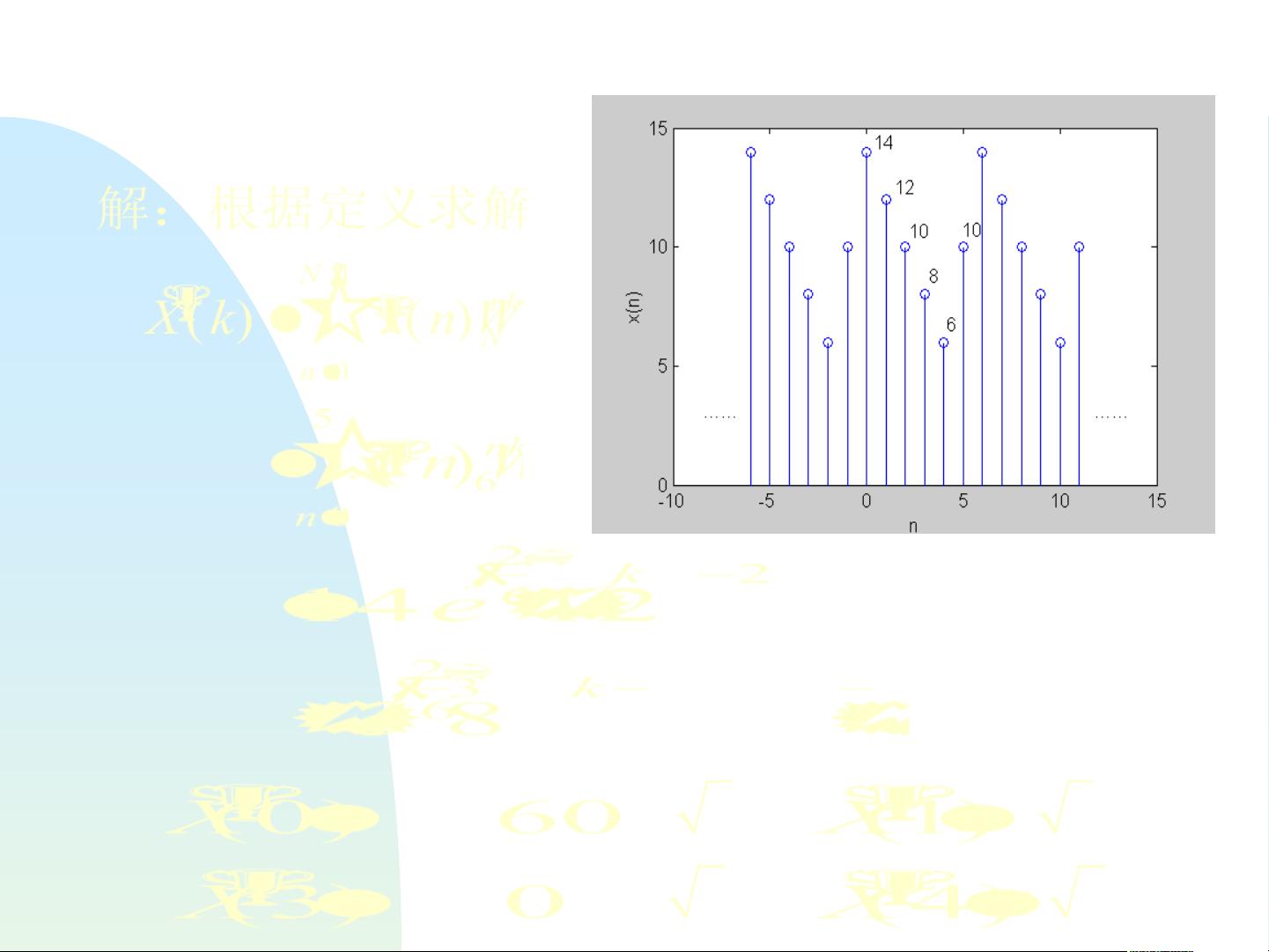
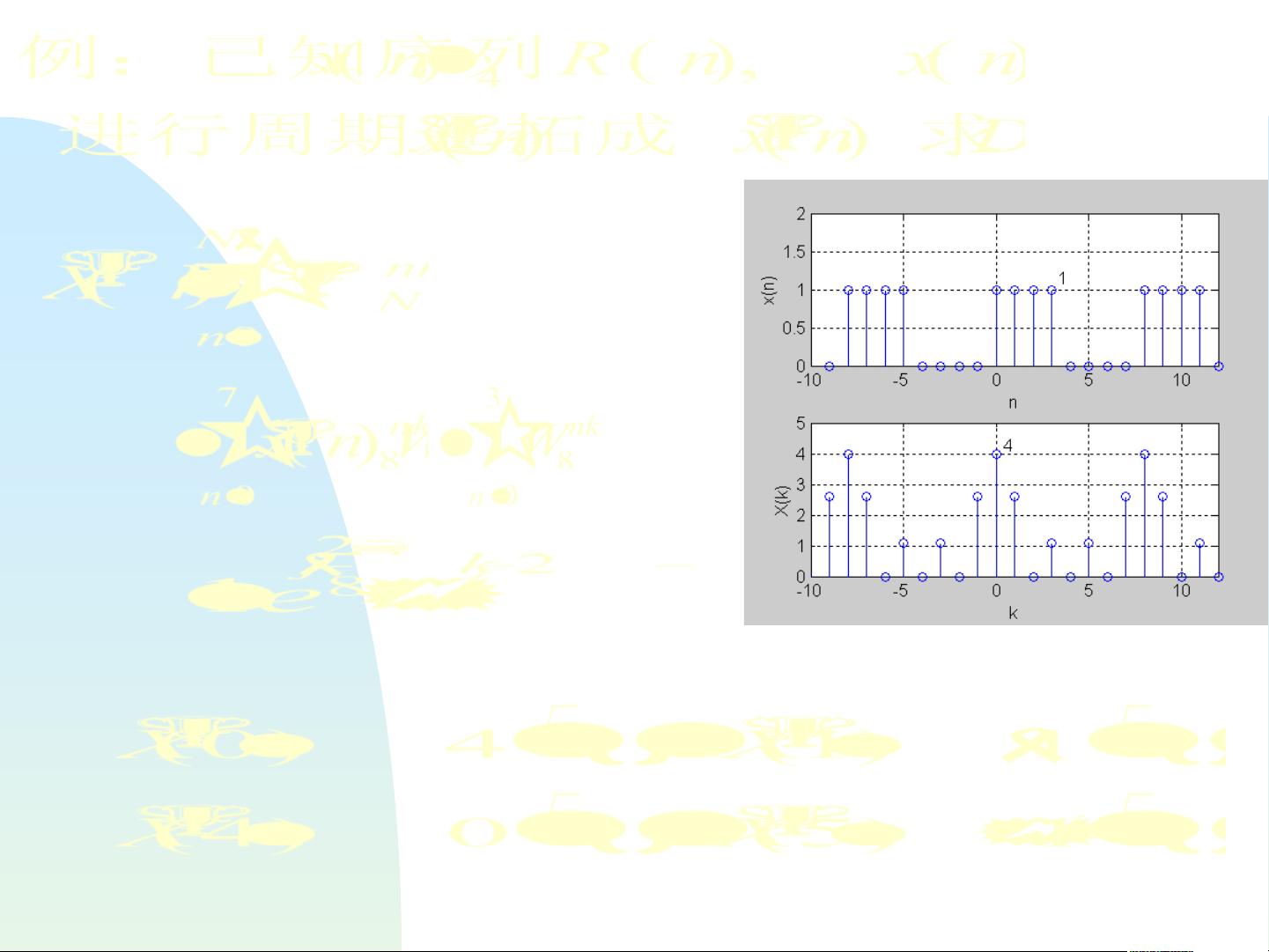
"数字信号处理：第三章 离散傅立叶变换.ppt" 本文主要探讨了数字信号处理中的核心概念——离散傅立叶变换（DFT），及其在不同时间-频率域中的表现形式。离散傅立叶变换是理解和分析离散时间信号的关键工具，对于数字信号处理领域具有重要意义。 首先，傅立叶变换是将信号从时域转换到频域的一种方法，有多种不同的形式。连续时间、连续频率的傅立叶变换（FT）用于分析非周期信号，它将信号表示为无限连续的频谱密度函数。而连续时间、离散频率的傅立叶级数（FS）则适用于周期信号，通过一系列离散频率成分来表示信号，每个频率对应一个幅度和相位。 离散时间、连续频率的序列傅立叶变换（DTFT）是离散信号的频域表示，它将离散时间序列映射到一个连续的频谱上。DTFT虽然给出了完整的频谱信息，但在实际应用中由于计算复杂度高，通常不直接用于计算。 离散傅立叶变换（DFT）是DTFT的一个重要特例，它只考虑有限长的离散序列，并且频谱也是离散的。DFT在数字信号处理中广泛应用，如滤波、频谱分析、卷积等。DFT的一些关键性质包括圆周移位、共轭对称性和频域抽样理论。圆周移位关系描述了信号在时域的移动如何影响其频谱；共轭对称性是关于DFT对称性的规则，对于实数序列，其DFT的共轭是对称的；频域抽样理论则解释了如何从有限的DFT点推断整个连续频谱。 此外，DFT还涉及卷积的概念，包括圆周卷积和线性卷积。圆周卷积是DFT运算中的卷积，而线性卷积是实际信号处理中更普遍的形式。两者之间的关系可以通过DFT和IDFT（逆离散傅立叶变换）来转换。序列的抽取与插值过程也是DFT的重要应用，它们分别用于减少数据量和提高采样率，从而适应不同的处理需求。 离散傅立叶变换是数字信号处理中的基石，它提供了分析和操作离散时间信号的强大工具。通过理解DFT及其各种性质，工程师和科学家可以有效地进行信号的频域分析，实现滤波、压缩、解码等各种信号处理任务。