ARIMA模型实战：非平稳序列识别与预测

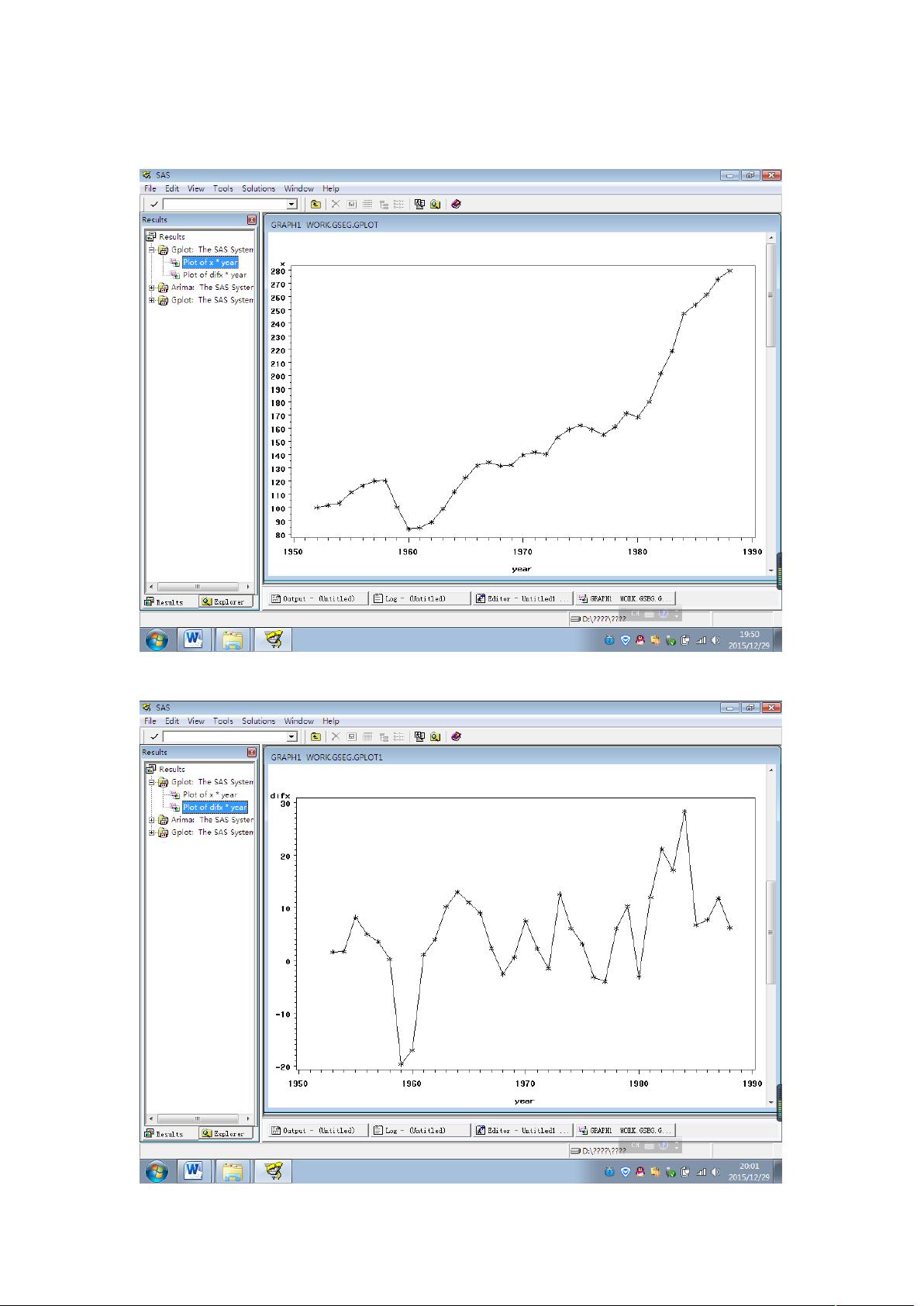
ARIMA模型是一种常用的时间序列分析方法，主要用于处理非平稳序列，通过差分、自相关函数(ACF)和偏自相关函数(PACF)来确定模型的形式。本例题详细展示了如何通过几个关键步骤来应用ARIMA模型进行分析。 首先，从给定的时序图开始，观察到序列存在显著的趋势，这表明序列是非平稳的。为了使序列变得平稳，需要对其进行差分处理。通过差分后的时序图，我们发现序列在均值附近稳定，且自相关图显示存在较强的短期相关性，这提示我们可能需要进行1阶差分。自相关系数一阶截尾，进一步支持了这一选择。 接着，进行白噪声检验以确认差分后的序列是否已经变得无趋势且无剩余的周期性。在这个例子中，P值小于0.05，意味着差分后的序列不是白噪声，即包含可解释的信息，不能简单地假设是随机噪音。 针对平稳非白噪序列，注意到1阶差分后的偏自相关图显示出了显著的不截尾性，这意味着ARMA模型可能不适合，因为ARMA模型通常假设PACF在滞后若干步后迅速衰减为零。在这种情况下，我们选择采用移动平均(MA)模型，具体来说是MA(1)，来拟合1阶差分后的序列。因此，最终的ARIMA模型形式为ARIMA(0,1,1)，即不包含自回归项但有一个差分项和一个移动平均项。 为了验证模型的拟合效果，对残差序列进行了进一步的统计检验，这部分细节并未在提供的部分中展示，但一般会检查残差的独立性、正态性和方差齐性。如果满足这些条件，模型的拟合就相对较好。 最后，利用拟合的ARIMA模型进行预测，结果存储在名为"res"的工作表中。给出的程序展示了如何使用SAS语言（如PROC ARIMA和PROC GPLOT）进行模型构建和预测，包括数据预处理（dif()函数）、模型估计（estimateq=1）、残差分析以及对未来五年的预测值及其置信区间（UCL和LCL）的图形展示。 总结来说，这个ARIMA模型例题涵盖了从序列非平稳性检测、差分操作、模型选择到预测的完整流程，展示了如何根据ACF和PACF图形、自相关检验以及残差分析来确定模型参数，并用实际代码展示了模型的实施。这有助于理解ARIMA模型在时间序列分析中的应用和实践。