四种进制转换表：二、八、十、十六进制详解

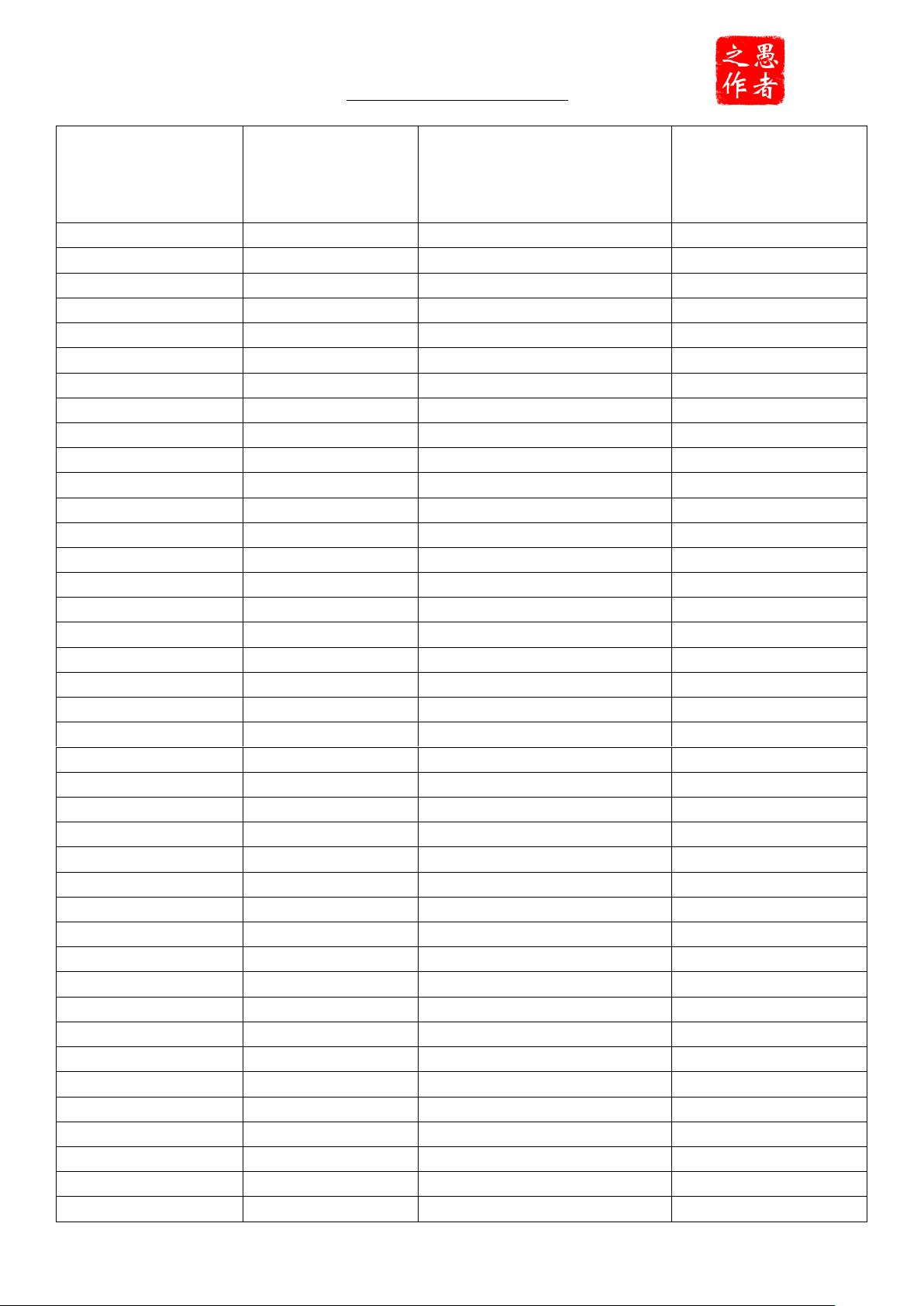
"愚者黑科技工作室资料1号提供了四种进制——二进制、八进制、十进制和十六进制之间的转换对照表，方便理解和操作不同进制之间的数值转换。" 在计算机科学中，不同的进制系统用于表示数字，每种进制有其特定的用途和优势。以下是这四种进制系统的详细说明： 1. **二进制（Binary System）**： - 二进制是最基础的数字系统，只包含两个数字：0和1。 - 在计算机中，所有数据和指令最终都会被转换为二进制形式，因为计算机电路能够轻松地识别和处理这种简单的数字系统。 - 二进制常用于位运算，如AND、OR和NOT，以及逻辑表达式。 2. **八进制（Octonary Number System）**： - 八进制由0到7这八个数字组成，通常用前缀`0o`或`0`表示。 - 八进制是二进制的便捷表示，因为每个八进制数字可以表示三个二进制位，方便简化较长的二进制数。 - 在早期的编程语言中，八进制常用来表示内存地址和权限控制。 3. **十进制（Decimal System）**： - 我们日常生活中最常用的进制，包括0到9这十个数字。 - 十进制是我们理解和交流数字的主要方式，大多数计算和测量都是基于十进制进行的。 4. **十六进制（Hexadecimal）**： - 十六进制由0到9以及A到F（代表10到15）这十六个数字组成，通常用前缀`0x`表示。 - 十六进制是二进制的一种紧凑表示，每个十六进制数可以表示四个二进制位，简化了在编程和调试中对二进制数的处理。 - 在编程中，十六进制常用于颜色编码、内存地址和网络地址等。 对照表展示了不同进制间的数值对应关系，例如，十进制的10在二进制中表示为`00001010`，在八进制中表示为`0A`，在十六进制中表示为`0A`。这种转换在编程和计算中非常重要，特别是在涉及到数据存储、计算和通信时。 理解并熟练掌握这些进制转换对于任何IT专业人员来说都是基础技能，无论是编程、网络还是硬件设计，都需要灵活运用不同进制之间的转换。例如，开发者可能需要将用户输入的十进制数值转换为二进制来存储，或者将十六进制颜色代码解析为RGB值。因此，熟悉这些进制系统及其转换是提升工作效率和解决问题的关键。