数字逻辑实践：七进制到十一进制计数器设计

"该资源是一系列关于数字逻辑的练习题，涵盖了如何使用特定逻辑器件实现不同进制计数器、构建大容量RAM和ROM的方法，以及相关电路分析。" 在这些练习题中，我们首先看到如何用十进制计数器74160实现一个六进制计数器。74160是一款十进制同步加法计数器，具有四个输出Q0到Q3。为了将其转化为六进制计数器，我们需要对计数器的输出进行适当的逻辑操作。通常，这可能涉及到对输入信号的控制，例如使能（CP）和清除（R）引脚的使用，以及可能的预置值（PRE或LOAD）来设置初始状态。题目并未给出具体的逻辑设计，但通常会涉及利用计数器的模运算特性。 其次，讨论了如何用512M×1位的RAM芯片构建512M×4位的RAM。在这个问题中，我们需要将单个位宽的RAM扩展为四位宽。这通常通过并联多个芯片来实现，每个芯片提供一个数据位，总共有四个芯片来存储四位数据。地址线（如A0到A28）会被复用，而数据线（D0到D3）则对应每个RAM芯片的数据输入/输出。同时，读写控制（R/W和CS）也需要相应扩展，以便同时操作所有芯片。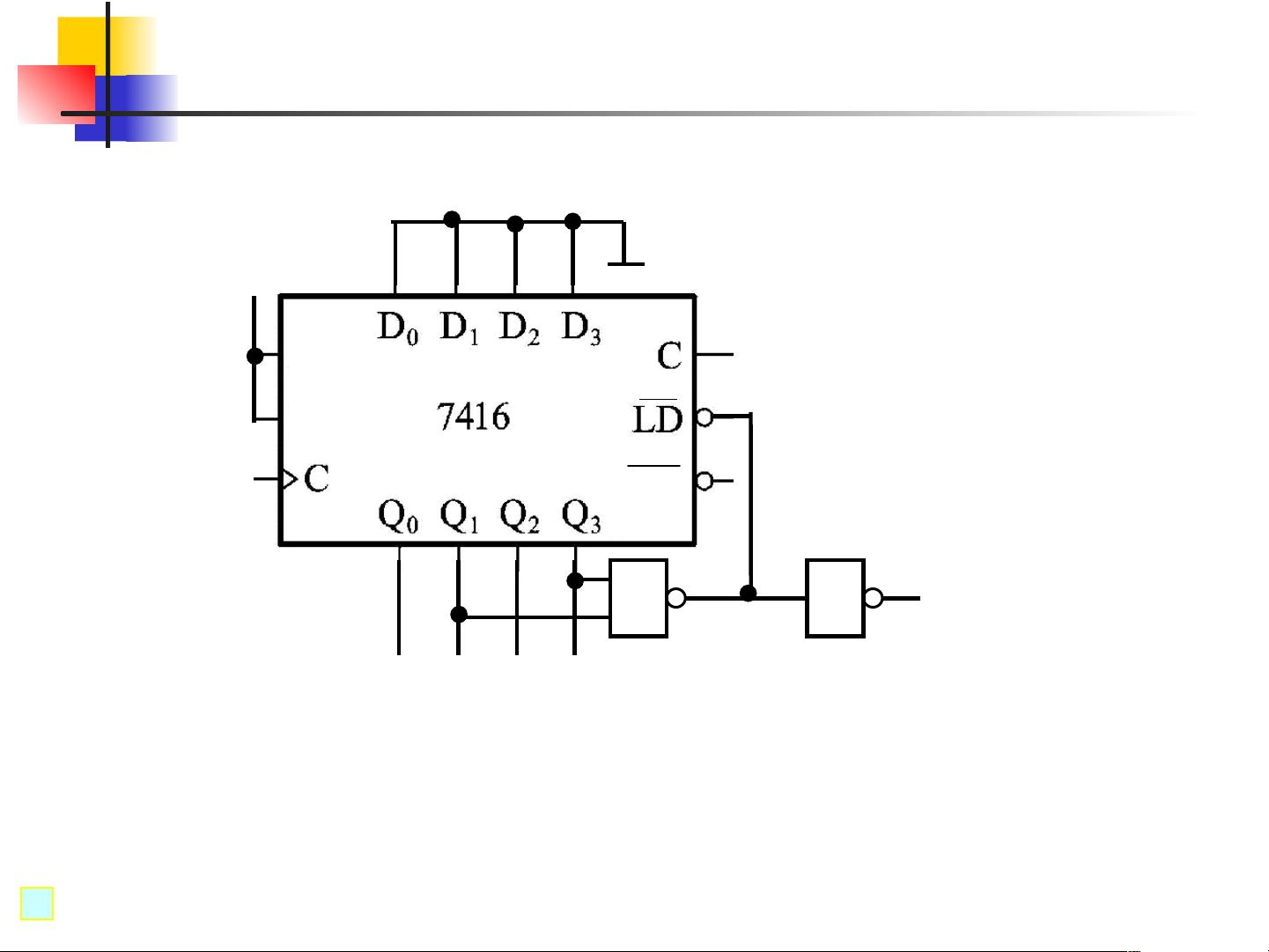 接着，提到了使用74HC163构成十一进制计数器。74HC163是一款四位同步二进制计数器，具有计数脉冲输入（CP）和预置输入（P、C）。要构建非二进制计数器，通常需要通过门电路（如与门、或门和非门）对计数器的输出进行编码，使其能够计数到指定的基数。在这个例子中，电路可能需要经过精心设计，以在特定的计数状态下触发进位信号，从而实现十一进制计数。 最后，探讨了如何使用128K×8位的ROM芯片构建512K×8位的ROM。构建更大容量的ROM需要将多个较小的ROM芯片串联起来，扩展地址线。由于128K×8位ROM的地址范围是128K(即2^17)位，而512K×8位ROM需要2^19位地址，因此需要增加两个额外的地址线（如A17和A18），并将它们通过译码器分配给各个ROM芯片。数据线（D0到D7）保持不变，而读/写控制线（R/W和OE）也需要扩展以控制每个ROM芯片。 这些练习题涵盖了数字逻辑设计的基础知识，包括计数器的设计、RAM和ROM的扩展、以及进制转换和地址译码等概念。通过解决这些问题，学生可以深入理解数字逻辑系统中的数据存储和处理机制。