量子启发布谷鸟算法解决无等待流水线调度难题
88 浏览量
更新于2024-08-27
收藏 1.85MB PDF 举报
无量子流水车间调度的量子布谷鸟联合搜索算法是一项针对No-Wait Flow Shop Scheduling (NWFSP)问题的研究，该问题在多个行业中具有广泛应用，如制造业和物流管理，其目标是优化生产周期时间（Makespan），即从开始到所有任务完成所需的最短时间。然而，由于NWFSP问题被证明为NP-hard，即在多项式时间内找到最优解非常困难，因此研究人员寻求高效的算法来近似解决。
该研究论文发表于2018年9月20日的《应用智能》期刊，由Haihong Zhu、Xuemei Qi等人共同署名，他们提出了一种新颖的量子启发式算法——量子布谷鸟协同搜索（Quantum Cuckoo Search, QCCS）。QCCS算法主要分为三个核心步骤：
1. **量子解决方案表示**：首先，通过将问题的解空间映射到量子系统中的状态，将传统的决策变量编码为量子比特的叠加态，这种量子化的方法有助于捕捉问题的复杂性，并可能提供潜在的搜索优势。
2. **量子启发式布谷鸟搜索与差分进化**（Quantum-Inspired Cuckoo Search-Differential Evolution, QCS-DE）：这部分引入了量子搜索的灵感，结合了布谷鸟算法的随机性和差分进化策略的全局搜索能力。布谷鸟算法模仿鸟类行为，通过随机的巢穴替换策略来探索解空间，而差分进化则通过生成并评估新的解来寻找最优解。
3. **局部邻域搜索**（Local Neighborhood Search, LNS）：为了防止陷入局部最优，算法还包含了局部搜索阶段，通过在附近区域进行微调，以进一步提高搜索效率和解决方案的质量。
论文作者对QCCS算法的收敛性进行了理论分析，确保了算法在求解过程中能够稳定且有效地逼近最优解。为了优化算法参数，论文还设计了Taguchi实验，这是一种统计实验设计方法，用于确定最合适的算法参数组合。
作者通过比较QCCS算法与当前最先进的算法，如GA-VNS（Genetic Algorithm with Variable Neighborhood Search）、HGA（Hybrid Genetic Algorithm）和TS-P（Tabu Search with Perturbation），展示了新算法在Recand Car基准实例上的性能。这些实例通常用于测试此类优化问题算法的性能，结果显示QCCS在处理NWFSP问题时展现出优越的性能和计算效率。
这篇研究不仅提出了一个创新的无量子流水线调度算法，还提供了理论支持和实证验证，对于优化复杂工业生产流程的求解策略具有重要的理论和实践价值。
Quantum-inspired cuckoo co-search algorithm... 793
presented in Section 3. To validate the convergence of the
QCCS algorithm, the convergence analysis is provided in
Section 4. Experimental results are illustrated in Section 5.
Finally, we conclude the paper and give several future
remarks in Section 6.
2 Problem formulation
In this section, we present the formal description of the
problem. The notations to be used in this paper are given in
Table 1 with explanation.
Based on the notations, we denoted the minimization
of the makespan as F
m
|nwt|C
max
, which is described as
follows. There are n jobs (J
1
,J
2
, ...,J
n
) that need to be
processed on m machines (M
1
,M
2
, ...,M
m
) in the same
order without any preemption and interruption, i.e., once a
job is started on the first machine, it has to be continuously
processed through m machines without interruption. At any
moment, job J
i
(1 ≤ i ≤ n) is being processed at most by
one machine, and machine M
k
(1 ≤ k ≤ m) can execute no
more than one job at a particular time. To satisfy the no-wait
constraint, the start of a job on the first machine must be
delayed. The objective of this problem is to find a feasible
schedule π = (π
1
,π
2
, ...,π
n
) for the n jobs such that the
makespan C
max
(π) is minimized, where C
max
(π) is also
equivalent to the finishing time of the last job on the last
machine, and is obtained using the following equation
C
max
(π) =
n
k=2
D
π
k−1
,π
k
+
m
j=1
P
π
n
,j
(1)
The no-wait constraints of the problem ensure that the
completion time distance between two adjacent jobs is
determined by the processing times of two jobs, regardless
of the other jobs in the permutation. Therefore, a completion
time distance is defined between each pair of jobs. The
completion time distance between two adjacent jobs, π
k−1
and π
k
, is calculated by
D
π
k−1
,π
k
= max
1≤i≤m
⎧
⎨
⎩
i
j=1
P
π
k−1
,j
−
i
j=2
P
π
k
,j−1
⎫
⎬
⎭
,k = 2, 3, ...,n.(2)
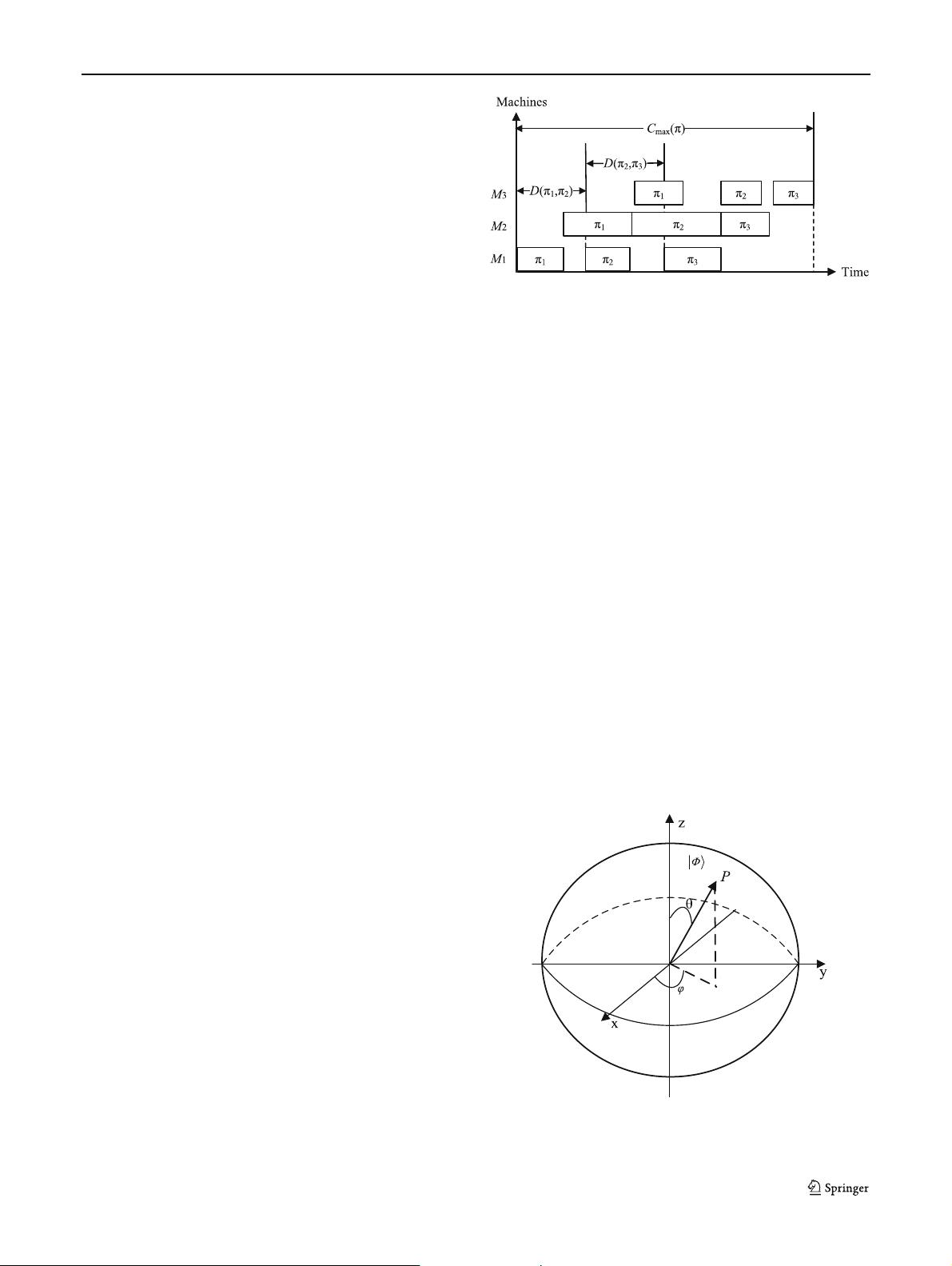
To provide a better understanding of the problem, we
present a Gantt chart of a no-wait flow-shop scheduling with
three machines and three jobs. It is clear that the C
max
(π)
can be easily obtained by summing up the completion time
distances (D
π
1
,π
2
,D
π
2
,π
3
) and the processing total time
3
j=1
P
π
3
,j
of these three jobs, as shown in Fig. 1.
Fig. 1 A Gantt chart of a no-wait flow shop scheduling
3 Quantum-inspired cuckoo co-search
(QCCS) algorithm
3.1 Quantum encoding based on Bloch coordinates
In quantum computation, the smallest unit of information is
expressed as a quantum bit which is also called a qubit. A
qubit can be represented by superposition of ’1’ state and
’0’ state in the Hilbert space. The state of a qubit is given by
|=cos(θ/2)|0+e
iϕ
sin(θ/2)|1 (3)
where θ and ϕ define a point P on Bloch sphere. A qubit
description on the Bloch sphere is shown in Fig. 2.
Therefore, a qubit is expressed as |=
[cos ϕ sin θ sin ϕ sin θ cos θ ]
T
by Bloch coordinates. The
Bloch coordinate encoding of the qubit is directly used
to generate cuckoo populations in QCCS algorithm. The
population q is given by
q =
⎛
⎝
cos(ϕ
1
) sin (θ
1
) cos(ϕ
2
) sin (θ
2
) ... cos(ϕ
n
) sin (θ
n
)
sin(ϕ
1
) sin(θ
1
) sin(ϕ
2
) sin(θ
2
) ... sin(ϕ
n
) sin (θ
n
)
cos(θ
1
) cos(θ
2
) ... cos(θ
n
)
⎞
⎠
(4)
Fig. 2 A qubit description on the Bloch sphere
剩余12页未读，继续阅读
177 浏览量
602 浏览量
115 浏览量
602 浏览量
297 浏览量
2021-07-18 上传
629 浏览量
245 浏览量
2025-01-06 上传
2025-01-06 上传
苹果虾丸
- 粉丝: 3
- 资源: 871
我的内容管理
展开
