动态规划DP详解:线性DP与实例解析
需积分: 0 63 浏览量
更新于2024-06-20
收藏 856KB PDF 举报
"线性DP详解,包括例题和练习,适用于C++编程"
线性动态规划(DP)是一种解决特定类型问题的优化技术,主要应用于计算机科学,特别是在算法设计中。线性DP的特点在于其状态之间的关系呈线性,即状态通常是基于一个线性范围来描述的,且状态转移相对简单,通常每个状态只依赖于少数其他状态。
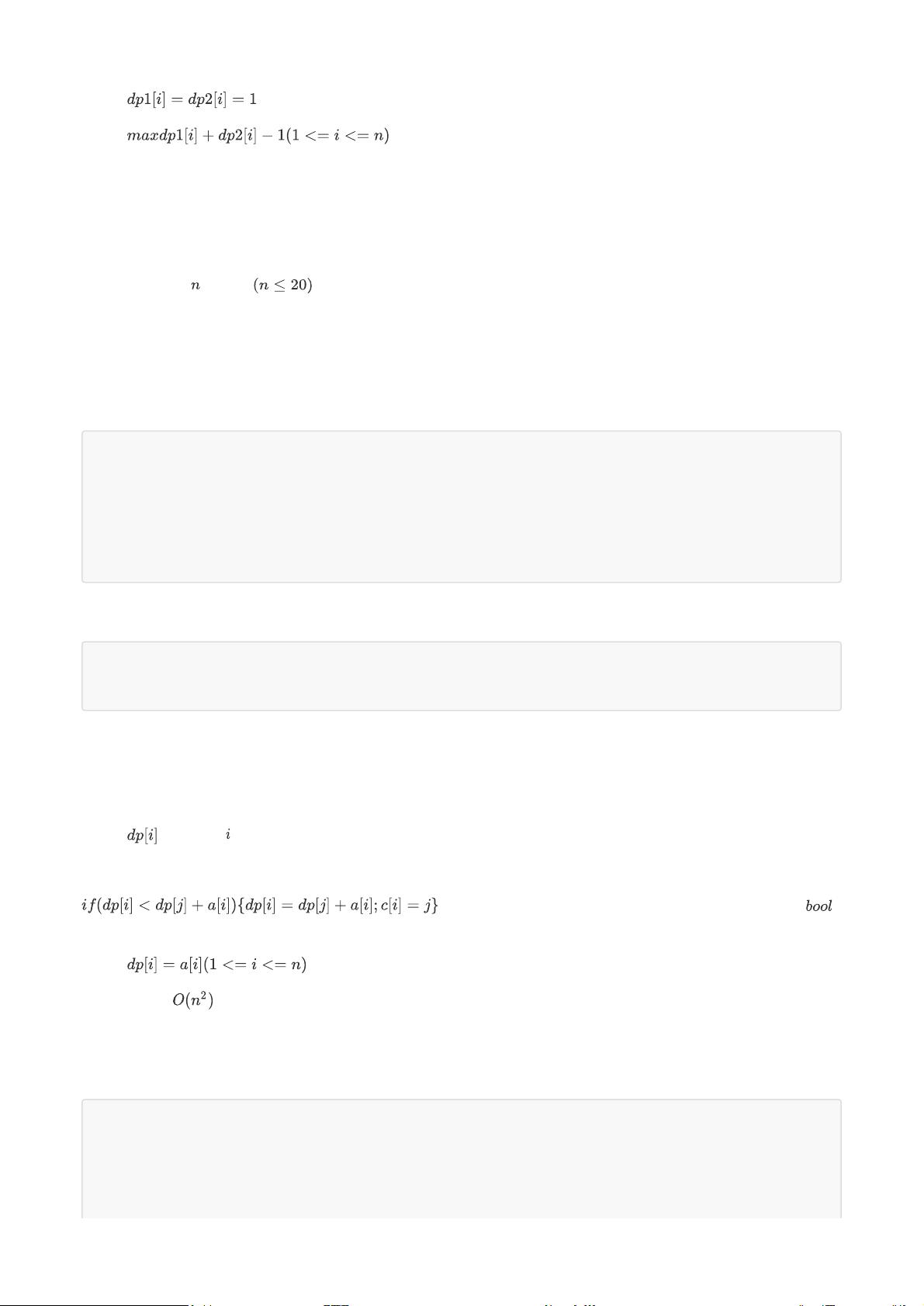
在动态规划问题中,状态是一个关键概念,它代表了问题在某个阶段的局部最优解。在线性DP中,状态通常由一个数组来表示,存储到当前阶段为止的最优值。例如,在导弹拦截问题中,状态`dp[i]`表示在考虑了第`i`发导弹之后,能够拦截的最长导弹序列。
导弹拦截问题的解题思路如下:
1. 定义状态:`dp[i]`表示考虑了第`i`发导弹后,最长不上升子序列的长度。
2. 初始化状态:`dp[0] = 1`,表示至少有一发导弹可以被拦截。
3. 状态转移方程:`dp[i] = max(dp[j])`,其中`j < i`且`导弹[j] >= 导弹[i]`。这意味着第`i`发导弹可以拦截的最长子序列是由所有不高于它的导弹构成的子序列中的最大长度。
4. 终止条件:`dp[n]`即为所求的最长拦截导弹序列的长度,其中`n`为导弹总数。
另一个例子是数字三角形问题,该问题要求找到从上至下经过数字和最大的路径。在这个问题中,状态`dp[i][j]`表示到达三角形中第`i`行第`j`列的最优路径和。状态转移涉及到两个方向:向左下和向下。通过比较左右两侧的路径和,选择较大的一个并更新当前状态。
线性DP的问题通常具有线性时间复杂度,如导弹拦截问题的时间复杂度为`O(n)`,其中`n`是导弹的数量。这是因为状态的数量与问题规模成正比,且每个状态只需要一次转移操作。
学习线性DP需要理解状态的定义、初始化、状态转移以及如何从这些元素构建有效的解决方案。通过例题的实践和练习,初学者可以更好地掌握这一概念,并将其应用到更广泛的动态规划问题中。
jiangchen_1234
- 粉丝: 1
- 资源: 1