东南大学机器人技术导论：第二章 数学基础

"东南大学的机器人技术导论课件，涵盖了机器人技术数学基础，特别是位置和姿态的表示、坐标变换和旋转矩阵等内容。" 在机器人学中，数学是理解和设计机器人系统的基础。本课件主要围绕第二章展开，深入探讨了机器人定位与定向的关键概念。首先，位置描述（Position）是指在三维空间中，一个点的位置可以用直角坐标系下的3x1列向量来表示，即位置矢量。 然后，方位描述（Orientation）或者姿态描述涉及的是空间物体的方向。通过坐标变换，我们可以描述一个物体相对于另一个坐标系的位置和方向。这通常通过旋转矩阵（Rotation Matrix）来实现，它是一个3x3的正交矩阵，表示了一个坐标系相对于另一个坐标系的旋转。例如，如果坐标系B是通过绕坐标系A的x、y、z轴旋转得到的，那么相应的旋转矩阵分别为简化的单位矩阵和包含方向余弦的矩阵。 旋转矩阵有一些重要的特性，例如它们是正交的，意味着旋转矩阵的逆矩阵等于其转置，即R^T = R^-1。这意味着通过旋转矩阵进行坐标变换后，可以很容易地恢复原坐标系的坐标值。此外，绕不同轴的旋转可以通过矩阵乘法组合，体现了坐标变换的复合性。 对于绕坐标轴的旋转，如绕Z轴的旋转，可以通过简单的几何推理得出旋转矩阵。例如，绕Z轴旋转后，X轴和Y轴的坐标会受到旋转角度的影响，而Z轴保持不变。这导致了旋转矩阵中的非对角线元素出现sin和cos函数，反映了坐标轴之间的相对旋转。 旋转矩阵的几何意义直观且实用，它可以描述刚体在空间中的旋转效应，如保持长度和方向不变的力矩传递。在机器人学中，这用于确定手臂或工具端点相对于基座或其他关节的精确位置和方向，从而控制机器人的运动。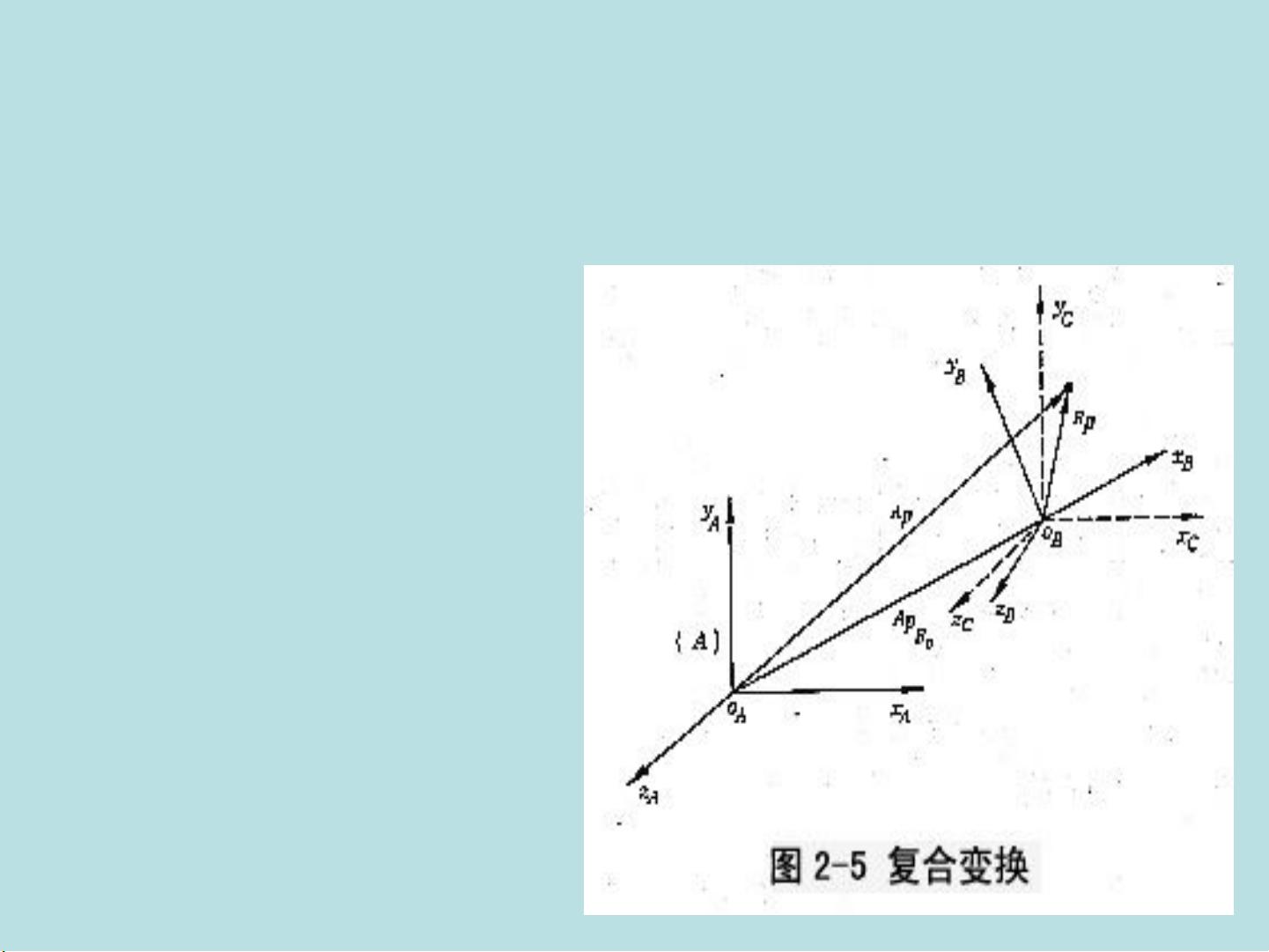 课件中的这部分内容还可能涉及如何通过齐次坐标变换（Homogeneous Transformation）将位置和姿态结合在一起，这对于描述机器人关节的连续运动特别有用。齐次坐标变换矩阵结合了旋转和平移，使得复杂的多关节运动可以简化为一系列简单的坐标变换。 这份东南大学的机器人技术导论课件第二章提供了机器人学基础的扎实讲解，包括位置和姿态的数学表达、坐标变换以及旋转矩阵的几何意义，这些都是机器人控制系统设计和运动规划中的核心概念。通过深入学习这部分内容，学生可以为后续更复杂的机器人动力学和控制理论打下坚实的基础。