MATLAB实现DFT与FFT实验分析

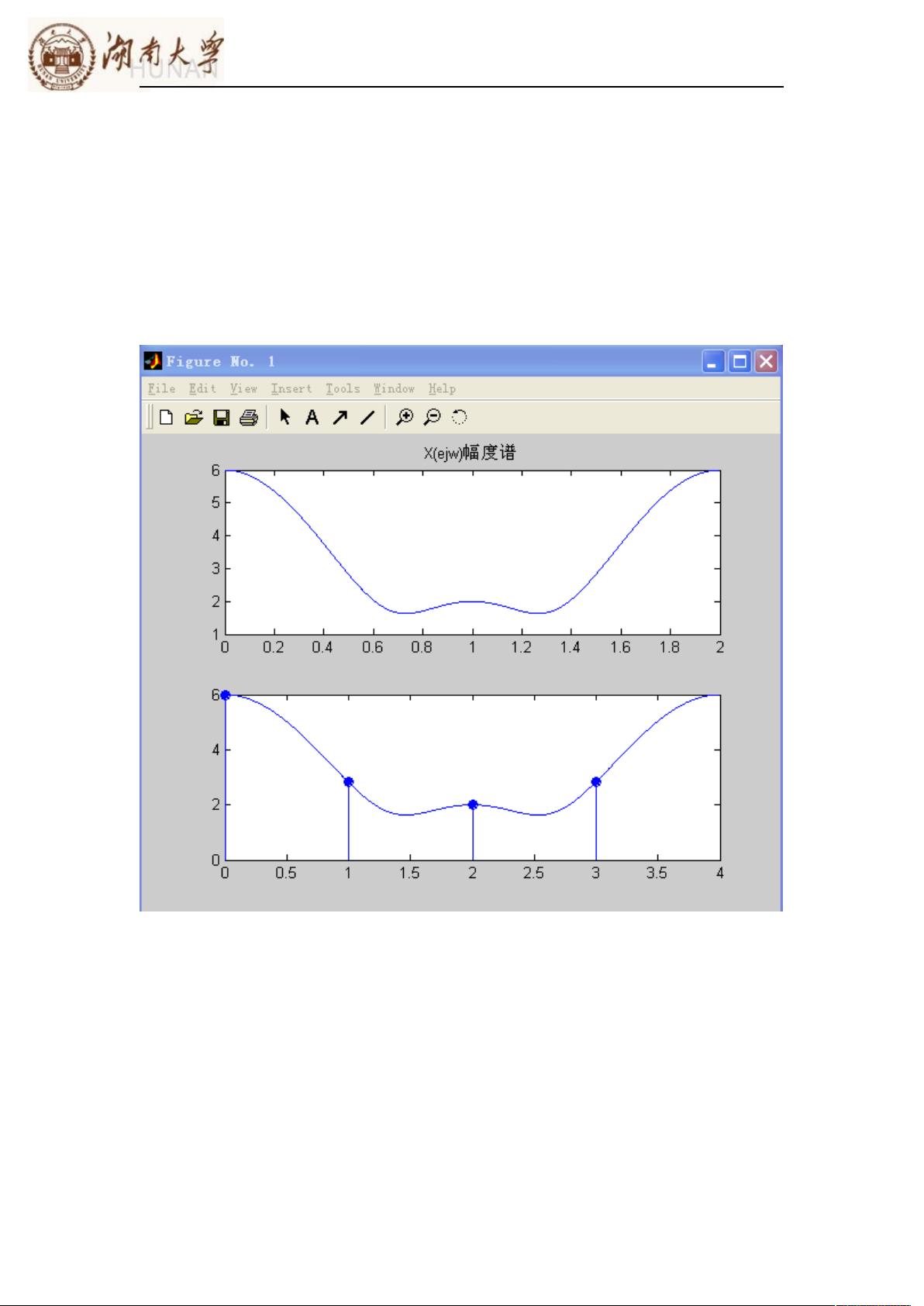
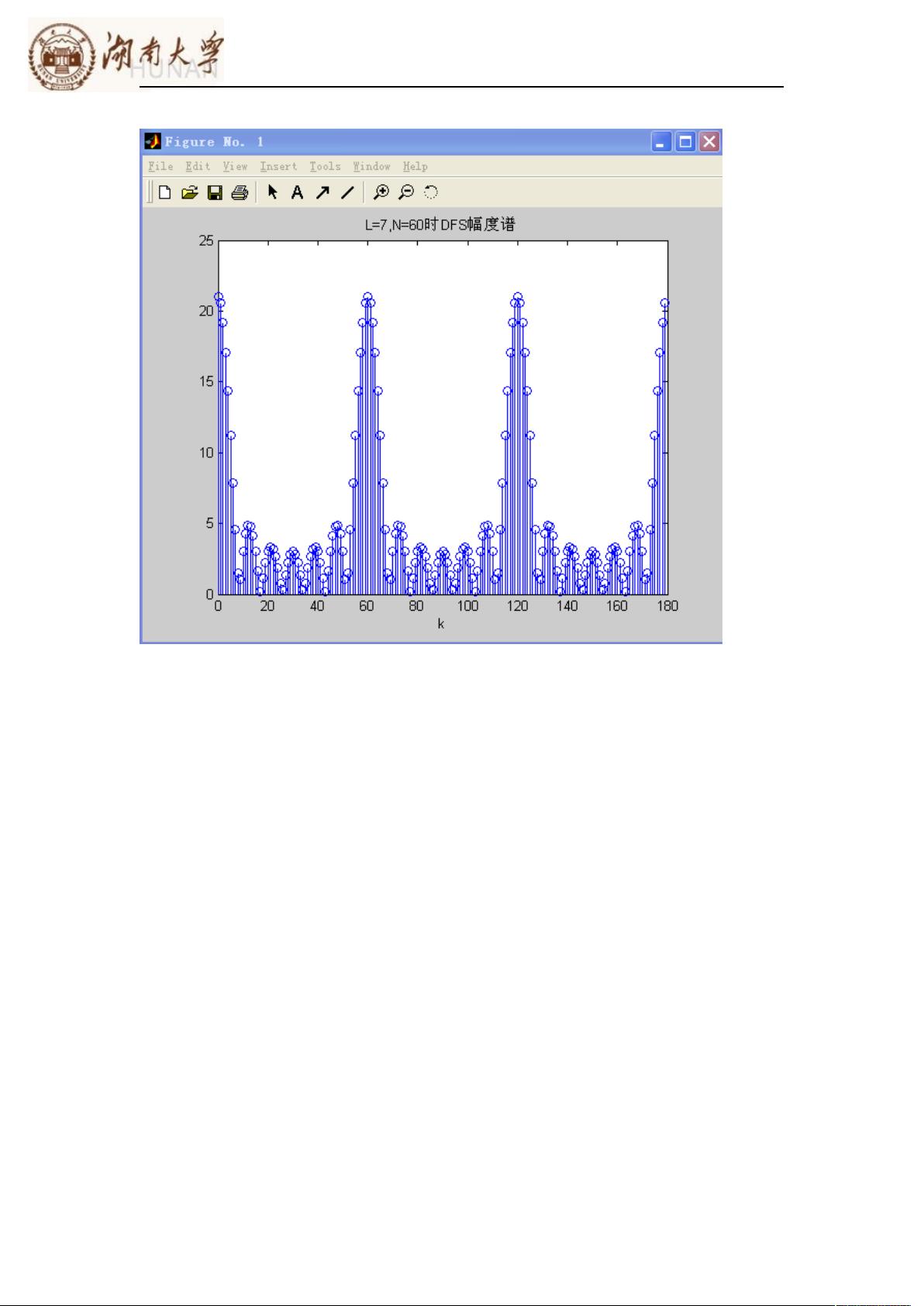
"数字信号处理文档，包含实验二DFT和FFT的详细内容，涉及周期序列DFS、DFT、FFT及Chirp-Z变换的理论与应用，使用MATLAB进行序列分析" 在数字信号处理领域，离散傅立叶变换（DFT）和快速傅立叶变换（FFT）是核心概念，广泛应用于信号的频谱分析。实验二“DFT和FFT”旨在深入理解这些概念及其计算方法。实验者通过学习和实践，不仅巩固了DFS（离散傅立叶级数）与DFT的理论基础，如旋转因子和序列性质，还掌握了快速傅立叶变换的不同算法，包括基2-FFT、混合基-FFT以及Chirp-Z变换。 实验内容首先要求计算周期序列的DFS，并通过MATLAB绘制幅度特性，展示周期序列的频谱特性。例如，序列{xn=0,1,2,3}是一个4点周期序列，通过DFT公式可以求得其DFS表示X(k)，并利用MATLAB的stem函数可视化幅度谱，从而直观理解DFS的性质。 接下来，实验者研究了周期方波序列，其中L代表基波周期内的高电平长度，N为总周期。实验中通过改变L和N的值，计算了DFS的幅度谱，揭示了N与频域抽样间隔的关系，以及占空比L/N对频谱结构的影响。例如，当L=5，N分别取20、40、60时，占空比变化导致频谱的周期性和零点带宽的变化。而当L=7，N=60时，这种关系同样适用。通过对这些结果的讨论，实验者能够总结出频谱特征与参数间的一般规律。 实验的第三部分涉及到有限长序列的处理，尽管这部分内容不完整，但可以推测会进一步探讨非周期序列的DFT和利用FFT进行频谱分析的方法。这通常包括序列的循环移位、循环卷积，以及如何利用DFT来揭示序列的频域特性。 这个数字信号处理的课程设计文档提供了一套完整的实践经验，帮助学生从理论到实践全面掌握DFT和FFT的核心知识，为后续的信号处理工作打下坚实基础。通过MATLAB编程，实验者能够亲自动手实现这些理论，增强对数字信号处理的理解和应用能力。