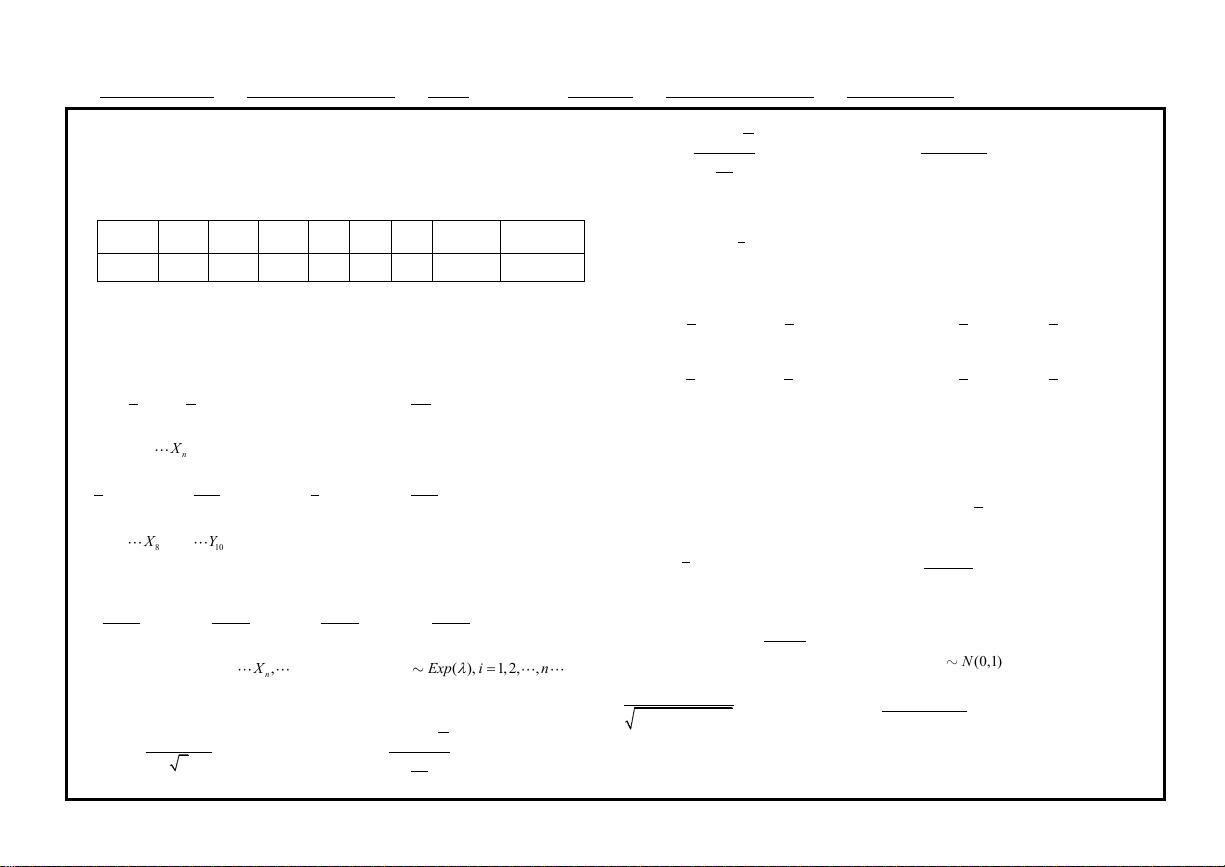
概率统计1：独立随机变量与正态分布应用

在《概率论与数理统计1》的这门课程中，涵盖了多个重要的概率和统计概念。以下是一些关键知识点的详细解析： 1. **事件概率关系**： - 题目1讨论了随机事件A和B的概率，考察了PA、PB以及它们之间的关系。如果AB表示A和B同时发生，题目要求确定PA和PB满足什么条件使得P(A|B)=P(A)，这是概率的独立性条件，即事件A的发生不受事件B的影响，即P(A|B) = P(A)。 2. **样本均值的无偏估计**： - 题目2涉及样本均值的估计。当样本X1, X2, ..., Xn来自均值为μ的总体，期望值E(X)已知时，无偏估计是指估计量的期望值等于真值μ。选项A不是无偏估计，因为它没有考虑n，而其他选项可能包含适当的样本平均数或加权平均，具体哪个选项正确取决于n和总体的性质。 3. **独立样本的F检验**： - 题目3涉及独立正态总体的样本方差的比较，通过F统计量来判断两个样本方差是否具有显著差异。F检验通常用于检验两组数据的变异程度是否相等，选项中可能是基于样本方差的某种比例作为F统计量的形式。 4. **随机变量序列的极限**： - 题目4关注的是随机变量序列的极限性质。当随机变量X1, X2, ...独立同分布且指数分布 Exp(i) 时，题目探讨了极限概率分布。选项A、B、C、D中可能涉及到样本均值的收敛性，极限分布可能是标准正态分布，即极限为正态分布的一部分。 5. **正态分布的参数估计**： - 最后，题目5讨论了正态分布零件长度的参数估计问题。在总体方差未知的情况下，通常采用样本方差来估计总体方差，抽取的16个零件长度的平均值可用于估计总体均值。具体计算可能涉及卡方分布或者t分布，这将根据样本大小和总体方差是否未知来确定。 这些题目涉及概率理论的基础概念，如事件概率、无偏估计、统计推断和正态分布参数估计，都是概率论与数理统计学习中的核心内容。理解和掌握这些知识点对于理解实际的统计分析和数据处理至关重要。