最小二乘法：多项式拟合的极值优化

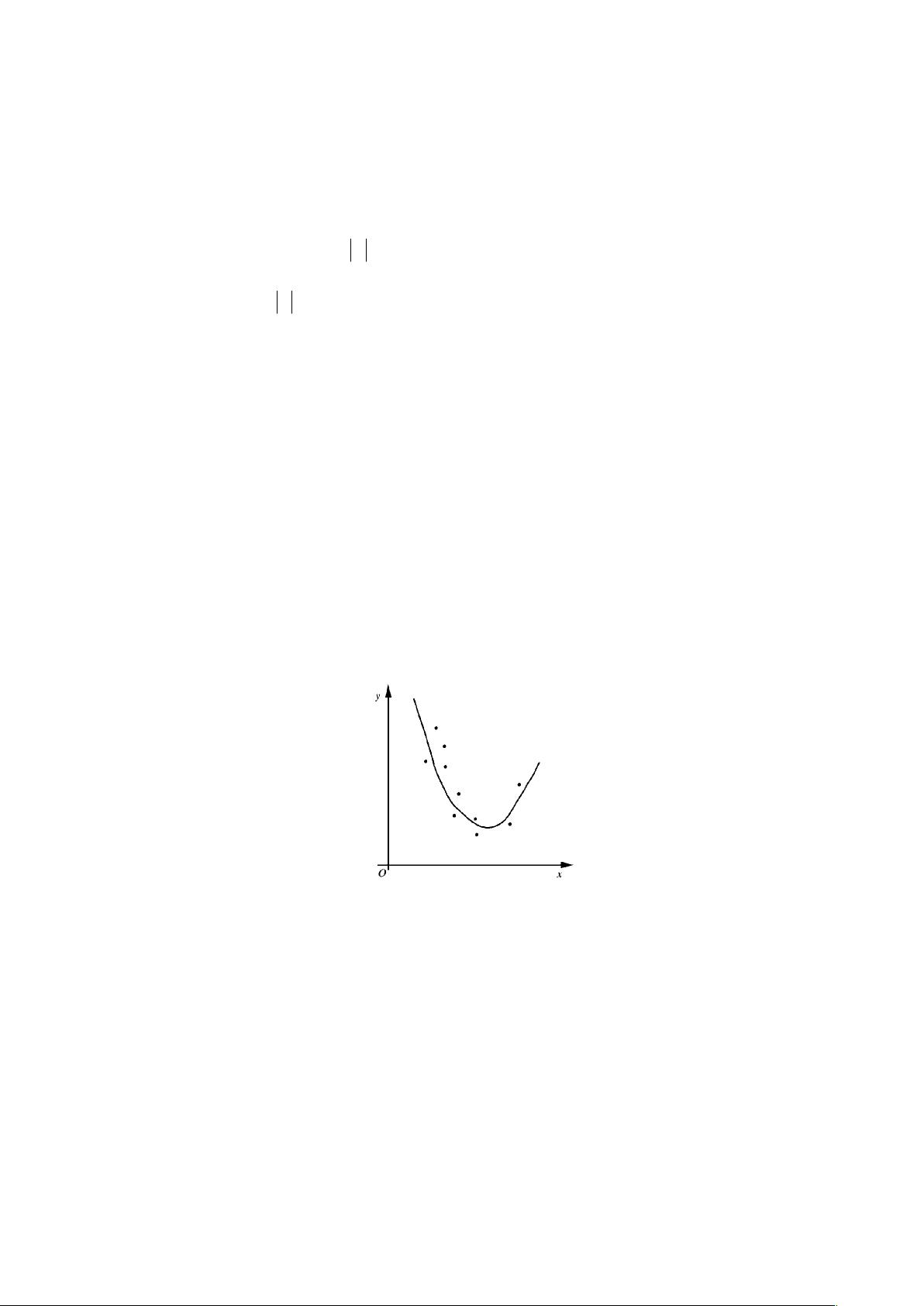
最小二乘法是一种统计学和数学优化技术，用于通过最小化误差平方和的方式来拟合数据点，使其与给定的数据尽可能地接近。这种方法在数据分析和模型构建中被广泛应用，特别是在曲线拟合领域。 一、最小二乘法的基本原理 最小二乘法的核心思想是找到一个函数，使得所有数据点到该函数的垂直距离（误差）的平方和最小。误差通常用2-范数衡量，即误差向量r的平方和的算术平方根。这种选择使得求解过程更便于微分运算，从而更容易得到最优解。在曲线拟合中，目标是寻找函数f，使得误差向量r满足\[ \sum_{i=0}^{m} (y_i - f(x_i))^2 \]最小。 二、多项式拟合 在具体应用中，多项式拟合是最常见的形式之一。假设有一组数据点\((x_0, y_0), (x_1, y_1), ..., (x_m, y_m)\)，我们考虑所有次数不超过n的多项式构成的函数类。我们的目标是找到一个多项式\( p(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n \)，使得数据点到多项式的偏差平方和最小，即满足\[ \min_{a_0, a_1, ..., a_n} \sum_{i=0}^{m} (y_i - (a_0 + a_1x_i + a_2x_i^2 + ... + a_nx_i^n))^2 \] 这个优化问题可以转化为多元函数的极值问题，对于每个\( a_k \)，我们有偏导数条件\[ \frac{\partial}{\partial a_k} \sum_{i=0}^{m} (y_i - p(x_i))^2 = 0 \]。这些条件组合形成一个线性方程组，即正规方程组或法方程组，可以表示为矩阵形式： \[ \begin{bmatrix} 1 & x_0 & x_0^2 & \cdots & x_0^n \\ 1 & x_1 & x_1^2 & \cdots & x_1^n \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_m & x_m^2 & \cdots & x_m^n \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_n \end{bmatrix} = \begin{bmatrix} y_0 \\ y_1 \\ \vdots \\ y_m \end{bmatrix} \] 由于系数矩阵是对称正定的，这意味着这个方程组有唯一解，从而确定了多项式\( p(x) \)的系数。最小二乘拟合多项式的平方误差\( \epsilon^2 \)可以用公式\[ \epsilon^2 = \sum_{i=0}^{m} (y_i - p(x_i))^2 \]来衡量。 总结来说，最小二乘法是一种强大的工具，用于根据给定数据点拟合出最佳的多项式模型。其关键在于解决线性方程组来找到系数，确保拟合函数能够最小化误差。这种方法不仅适用于多项式，也适用于其他函数类别的曲线拟合，并且因其简便性和有效性，在各种实际问题中扮演着重要角色。