图的生成树与生成森林详解：概念与存储结构

图的生成树和生成森林是图论中的核心概念，它们在描述网络结构、算法设计以及数据压缩等领域具有重要作用。在深入理解图的基本概念之前，先来了解一下什么是图。图G由两个基本元素组成：节点集合V和边集合E。节点（也称顶点或节点）是图中的基本单元，通常用整数标识，如1, 2, ..., n，表示节点之间的关系。边是连接节点的连接方式，用无序数对（u, v）表示，其中u和v是相连的节点，且边没有方向性，除非在有向图中。 在图中，节点的度数定义为与其相连的边的数量。对于简单图，每个节点的度数不能超过n-1，其中n是节点总数。图的大小通过边的数量|E|衡量，最大值为n*(n-1)/2，如果达到这个上限，图被称为完全图。 路径在图论中是关键概念，包括简单路径、简单圈（环）、连通性和非连通图。连通图意味着任何两个节点间存在路径，而非连通图则由若干个连通分量构成。路径还可以进一步区分是否相交，如不相交路径和严格不相交路径。 图的简单分类涉及多种类型，如无向图和有向图，前者关系是对称的，而后者边是有方向的。无权图和加权图的区别在于边是否带有权重，可以代表诸如费用、距离等实际意义。在无权图中，权重通常默认为1。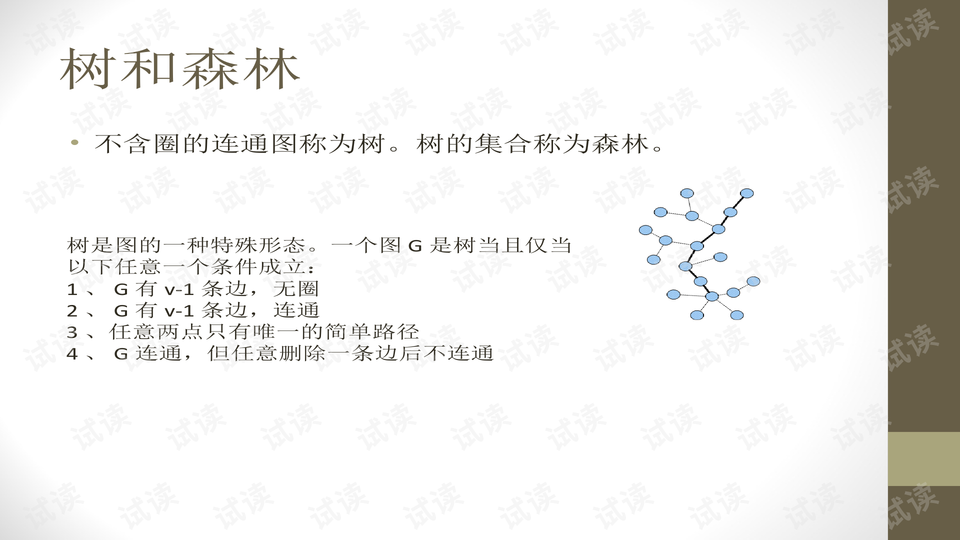 在这些概念之上，图的生成树和生成森林显得尤为重要。生成树是一个包含图G所有节点的最小树，即去掉图中的某些边后形成一棵树，使得所有节点仍可通过路径相连，且不存在环。生成树的性质常常用于求解最短路径问题。生成森林则是由多个生成树组成的集合，每个生成树对应图的一个连通分量。 理解图的生成树和生成森林有助于我们理解和设计各种算法，例如拓扑排序、 Kruskal's 或 Prim's 算法用于找到最小生成树，以及Fiedler's 耦合常数等在图的特征值分析中的应用。在实际问题中，这些概念的应用广泛，如网络设计、社交网络分析、计算机图形学等。掌握这些基础知识，对于深入研究图论和相关领域至关重要。