H.264 SVC 3-D Wavelet Coding Scheme in IEEE TCSVT专刊
需积分: 50 132 浏览量
更新于2024-12-19
收藏 1.6MB PDF 举报
"IEEE TCSVT H.264 SVC 专刊合集1，主要讨论了基于杠铃提升的3D小波编码方案，并与可伸缩视频编码（SVC）标准进行了比较分析。"
本篇文章是IEEE Transactions on Circuits and Systems for Video Technology期刊上的一篇邀请论文，主要探讨了一种被称为“杠铃提升”编码策略，该策略被MPEG临时工作组采纳为用于进一步探索小波视频编码的通用软件。H.264 SVC（可伸缩视频编码）是一种先进的视频编码标准，旨在提供灵活的视频流服务，适应不同的网络条件和终端能力。
杠铃提升编码方案的核心技术包括杠铃提升、分层运动编码、3D熵编码以及基层嵌入。杠铃提升是一种优化的小波变换技术，它可以提高编码效率并降低计算复杂度。分层运动编码则是对视频序列中的运动信息进行层次化处理，允许不同层之间共享信息，从而实现编码的可伸缩性。3D熵编码是利用三维空间结构来更有效地编码视频数据，提高压缩效率。而基层嵌入是指将基本编码层的信息嵌入到更高级别的层中，确保视频质量随层的增加而提高。
文章还深入分析了杠铃提升编码与即将推出的SVC标准之间的关系。SVC引入了层次化的时空预测技术，这与小波编码中的运动补偿时间提升（MCTF）有密切联系。作者对比了这两种方法的相似性和差异性，帮助读者更好地理解现代可伸缩视频编码技术的原理和特点。
尽管可伸缩视频编码在灵活性和适应性方面取得显著进步，但文章也指出了一些尚待解决的挑战，如空间可伸缩编码的性能问题以及运动补偿提升的精确性问题。这些问题的解决将有助于进一步提升视频编码的效率和质量，以满足不断增长的多媒体通信需求。
这篇文章为读者提供了关于H.264 SVC和杠铃提升编码技术的深入理解，同时也指出了当前可伸缩视频编码领域面临的技术挑战，对于从事视频编码和压缩研究的学者和工程师具有很高的参考价值。
1258 IEEE TRANSACTIONS ON CIRCUITS AND SYSTEMS FOR VIDEO TECHNOLOGY, VOL. 17, NO. 9, SEPTEMBER 2007
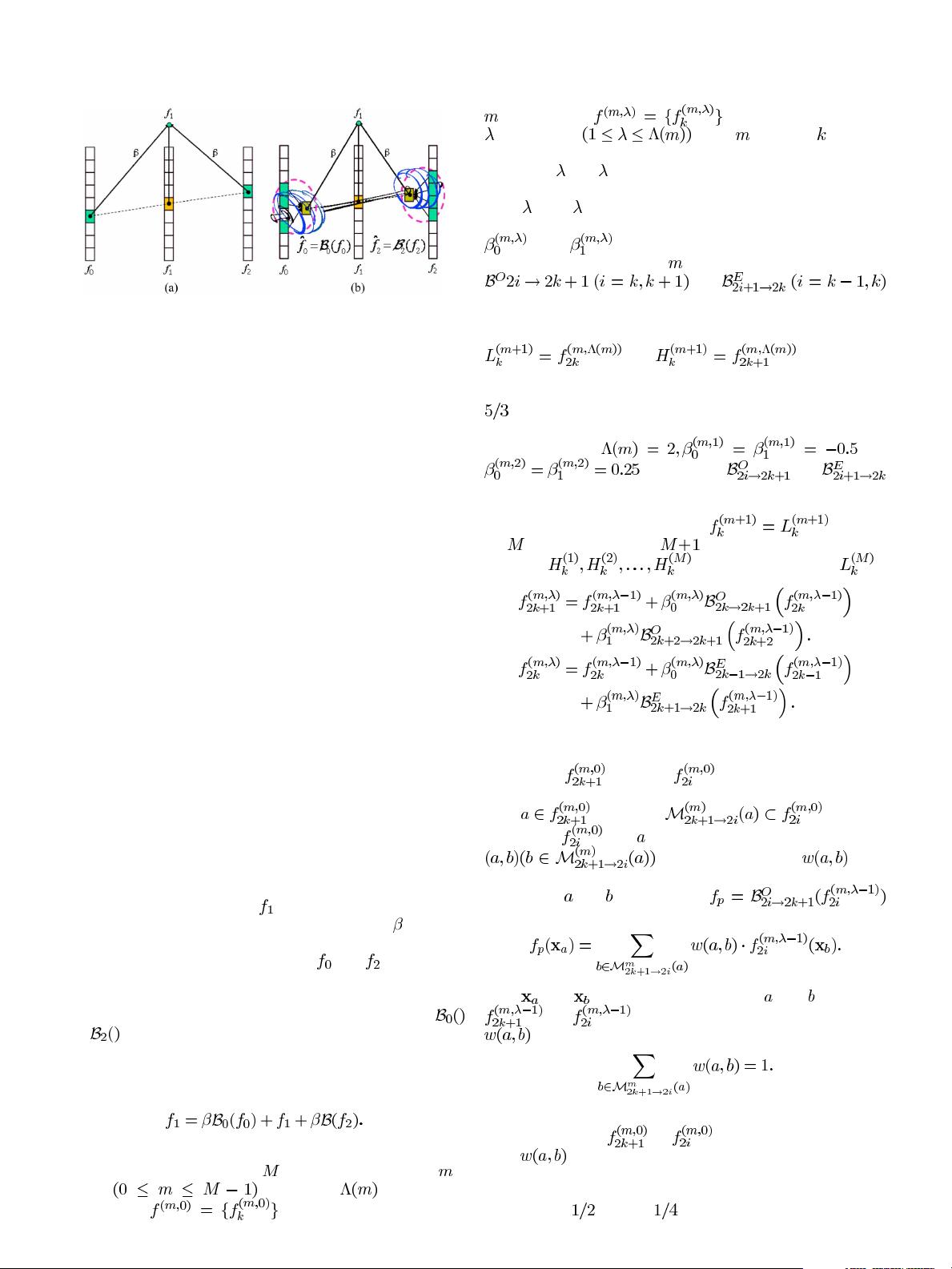
Fig. 2. Basic lifting step. (a) Conventional lifting. (b) Proposed Barbell lifting.
The following subsections will discuss the core techniques
employed in our proposed coding scheme, such as Barbell
lifting, layered motion coding, 3-D entropy coding and base
layer embedding. At the same time, we also cite several related
techniques used in other schemes so as to give audience a fuller
picture.
A. Barbell Lifting
In many previous 3-D wavelet coding schemes, the concept of
lifting-based 1-D wavelet transform is simply extended to tem-
poral direction as a transform along motion trajectories. In this
case, the temporal lifting is actually performed as if in 1-D signal
space. This requests an invertible one-to-one pixel mapping be-
tween neighboring frames so as to guarantee that the prediction
and update lifting steps operate on the same pixels. However, the
motion trajectories within real-world video sequences are not
always as regular as expected, and are sometimes even unavail-
able. For example, pixels with fractional-pixel motion vector are
mapped to “virtual pixels” on reference, which cannot be di-
rectly updated. In the case of multiple pixels mapping to one
pixel on reference, the related motion trajectories will merge.
For covered and uncovered regions, motion trajectories will dis-
appear and appear. The direct adoption of 1-D lifting in temporal
transform cannot naturally handle these situations. It motivates
us to develop a more general lifting scheme for 1-D wavelet
transform in a high-dimensional signal space, where multiple
predicting and updating signals are supported explicitly through
Barbell functions.
When the lifting scheme developed by Sweldens [36] is di-
rectly used in temporal direction, the basic lifting step can be il-
lustrated in Fig. 2(a). A frame
is replaced by superimposing
two neighboring frames on it with a scalar factor
specified
by the lifting representation of the temporal wavelet filter. No-
tice that only one pixel, of the signals
and respectively,
is involved in the lifting step. In the proposed Barbell lifting as
shown in Fig. 2(b), instead of using a single pixel, we use a func-
tion of a set of nearby pixels as the input. The functions
and are called as Barbell functions. They can be any linear
or nonlinear functions that take any pixel values on the frame
as variables. The Barbell function can also vary from pixel to
pixel. Therefore, the basic Barbell lift step is formulated as
(1)
According to the definition of basic Barbell lifting step, we
give a general formulation for
-level MCTF, where the th
MCTF
consists of lifting steps.
Assume that
denotes input frames of the
th MCTF and denotes the result of the
th lifting step of the th MCTF. indicates
the frame index.
For odd
, the th lifting step modifies odd-indexed frames
based on the even-indexed frames, as formulated in (2). For
even
, the th lifting step modifies even-indexed frames
based on the odd-indexed frames, as formulated in (3). Here
and are filter coefficients specified by the
lifting representation of the
th level temporal wavelet filter.
and
are the Barbell function operators to generate lifting signal
in odd and even steps, respectively. After all the lifting steps,
we get the lowpass frames and highpass frames, defined by
and , respectively.
Theoretically, arbitrary discrete wavelet filter can be adopted
in MCTF easily based on (2) and (3). But the biorthogonal
filter is the one which has already been verified prac-
tical with good coding performance so far. It consists of
two lifting steps:
and
. In this case, and
are commonly called as prediction and update steps, respec-
tively. In multilevel MCTF, the lowpass frames of a MCTF level
are fed to the next MCTF level by
. Finally,
the
-level MCTF outputs temporal subbands: highpass
subbands
, and lowpass subband
(2)
(3)
1) MC Prediction: We discuss the Barbell function of MC
prediction. Assume that there is a multiple-to-multiple mapping
from frame
to frame , based on the motion be-
tween these frames and the correlation in related pixels. For any
pixel
,wedefine as the set
of pixels in
that is mapped to. For each pair of pixels
, weighting parameter is in-
troduced for prediction, to indicate the correlation strength be-
tween pixel
and . The operator
based on Barbell lifting is defined as
(4)
Here
and are coordinates of pixels and , in frames
and , respectively. The weighting parameters
are subject to the constraint
There are two types of parameters in the Barbell function:
the mapping from
to and the weighting param-
eters
. The mapping can be derived from motion vec-
tors estimated based on the block-based motion model. In gen-
eral, motion vector is up to fractional pixel for accurate predic-
tion, such as
-pel and -pel in H.264/AVC. The Barbell
剩余13页未读，继续阅读
2011-12-10 上传
2008-07-07 上传
2021-08-11 上传
2023-11-21 上传
2021-03-25 上传
2021-03-25 上传
2021-02-04 上传
noter
- 粉丝: 29
- 资源: 1
我的内容管理
展开
