单摆与Duffing方程解析：入门到混沌运动

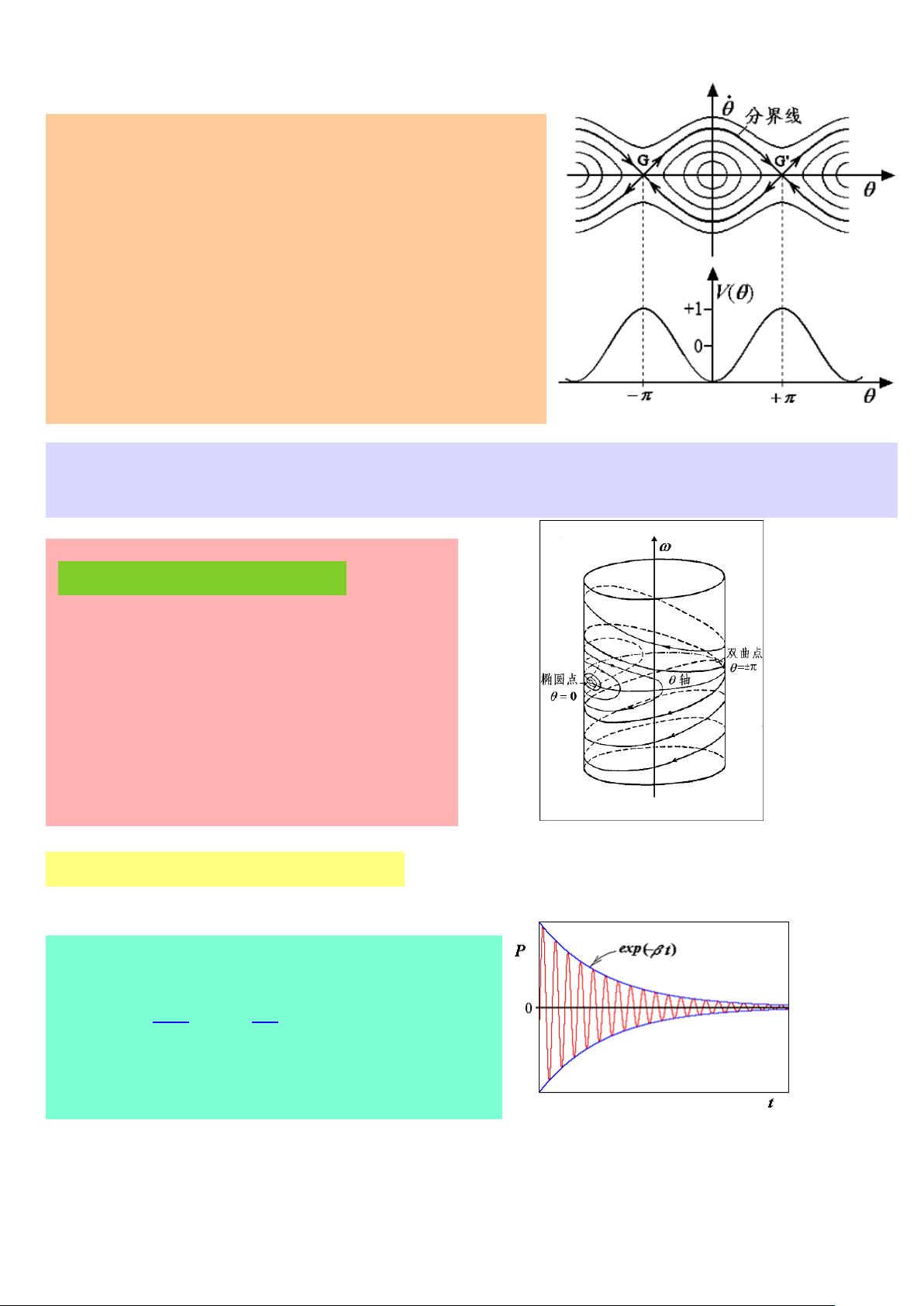
"本资源深入探讨了单摆与Duffing方程之间的关系，以帮助初学者理解这一复杂概念。单摆是经典力学中的一个基础模型，它描述了一个物体在重力作用下沿直线来回摆动的现象。在这个过程中，单摆的动力学方程被引入，考虑了摆长、质量、阻力、驱动力以及角位移等因素。阻力与速度成比例的情况被无量纲化处理，引入了ω0、mω0^2和mlω0^2作为基本量纲，简化了方程。 在无阻尼且无外部驱动力的情况下，即β=0且f=0，单摆的运动简化为纯简谐振动，其位移曲线呈现出典型正弦波形。当摆角变化超过一定范围（如10度至180度），运动性质会发生转变，从简谐振动变为周期运动或旋转运动，这取决于初始条件，如初速度。 相图是分析这类系统的重要工具，它描绘了摆角θ和角速度之间的关系随时间变化的轨迹。通过研究微分方程的系数和结构，可以在不求解方程的情况下预测系统的运动状态。将方程积分后，能量守恒体现在动能K（与dθ/dt有关）和势能V（与θ有关）的总和E中，椭圆点代表了系统的平衡状态，即摆角为0，角速度为0，系统的总能量为零。 Duffing方程在此基础上引入了非线性项，使得单摆的运动行为更加复杂，可能进入混沌状态，这是非线性动力学研究的核心内容之一。该资源以直观的方式引导读者理解单摆模型的扩展，并展示了如何通过无量纲化方法处理实际问题，这对于理解更高级的物理现象和工程应用具有重要意义。"