二叉树形态与数据结构习题解答

本资源主要涉及数据结构课程的课后习题答案，针对第三章的内容进行了深入解析。第一部分探讨了计算n个节点可以构成的不同二叉树形态的数量。这个问题涉及到二叉树的生成函数f(n)，其中f(1)=1，f(2)=2，并通过Catalan数的定义给出了递推公式：h(n)=h(n-1)*(4*n-2)/(n+1)。这个公式描述了n个节点形成平衡的二叉树，即每个节点的左子树和右子树的节点数差不超过1。 对于具体例子，如n=3，可以得到5种不同的形态。随着n的增加，这些形态的增长遵循Catalan数的规律。第二部分解答了关于特定数据集构造的二叉树中序遍历问题，指出有5种可能的二叉树结构，尽管它们的中序遍历结果相同。 第三部分关注的是二叉树的结构特征，例如树的深度、叶子节点和度数。若树深度为6，有17个叶子节点且度为1的节点为0，这提示了树的高度和结构分布。同样，如果一个二叉树有20个叶子节点，30个只有一个孩子的节点，可以通过计算得出总节点数为69。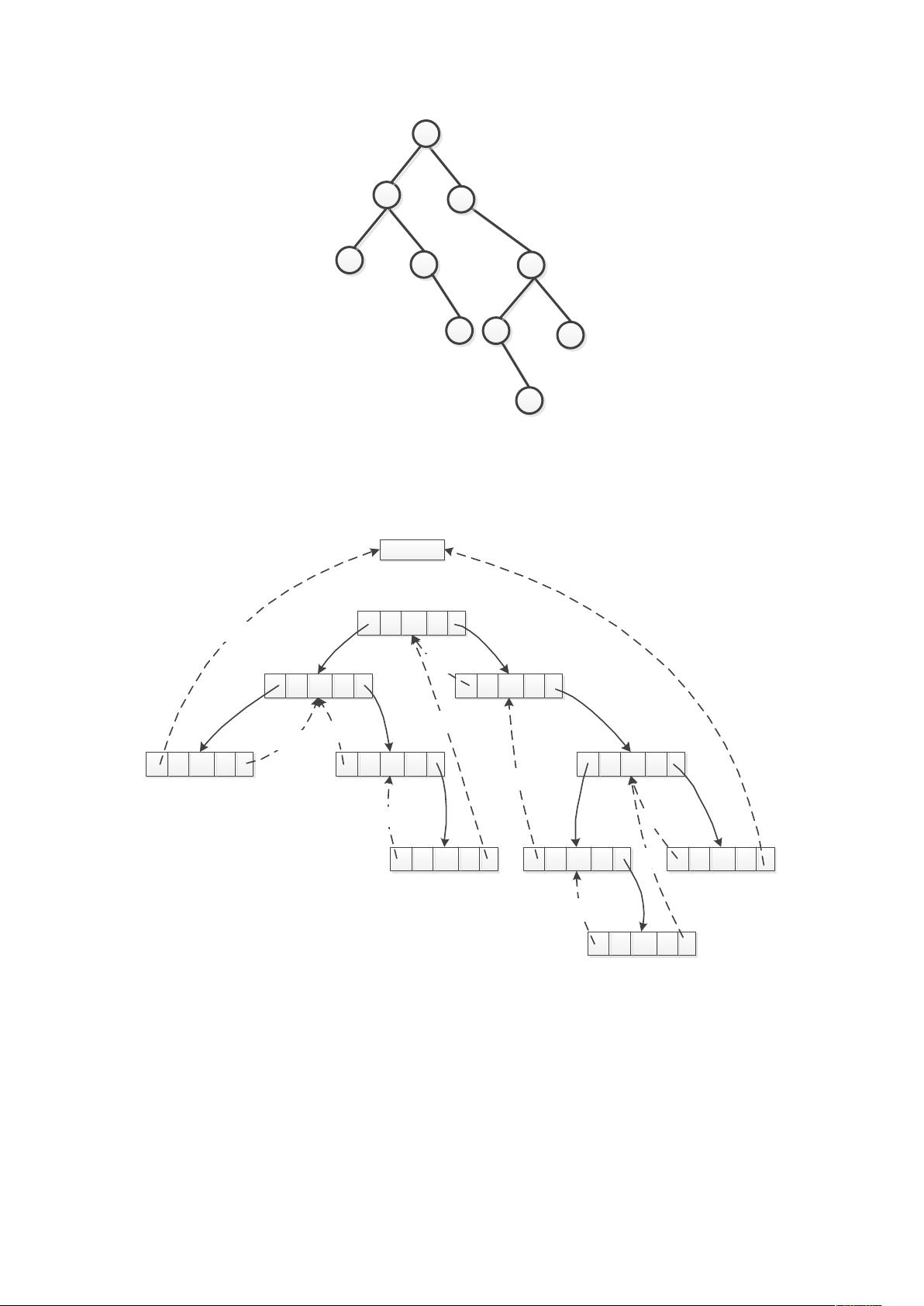 最后，针对中序线索二叉树，资源详细解释了如何在这样的数据结构中查找给定节点的前序后继和后序后继。前序后继的查找规则基于节点的ltag和rtag值，以及其与父节点的关系。如果节点没有左孩子，那么后继可能是右孩子；如果有右孩子但不是左孩子，后继可能是父节点的右孩子或者后续的中序节点；如果存在多个后继候选，需要顺着线索追踪直到找到满足条件的节点。 这份资料涵盖了数据结构中的核心概念，包括二叉树的计数、结构分析和中序线索二叉树的操作，对理解和实践数据结构非常有帮助。