神经网络优化：交叉熵代价函数的作用和公式推导

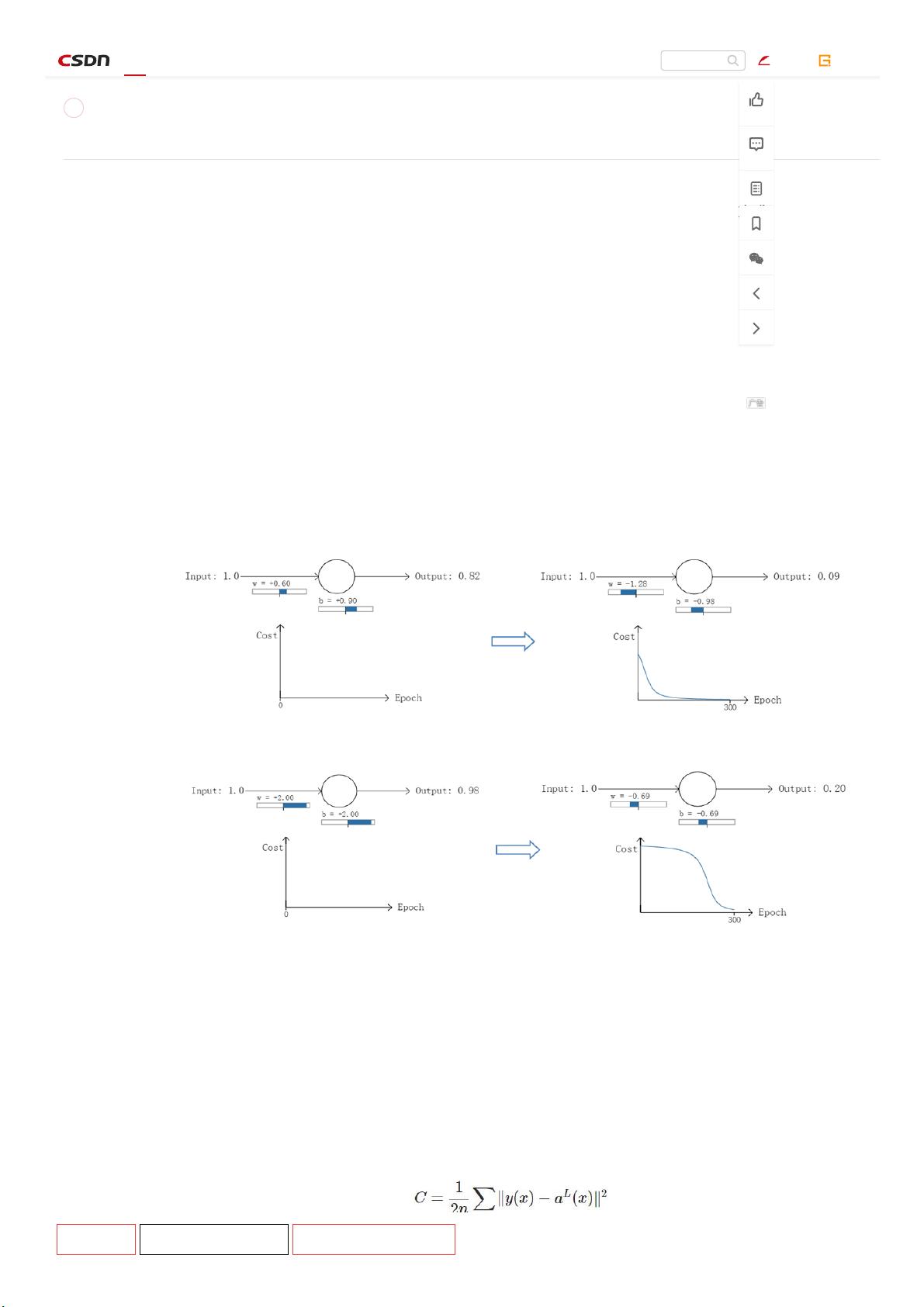
交叉熵代价函数的作用及公式推导 交叉熵代价函数（Cross-entropy cost function）是一种用于衡量人工神经网络（ANN）预测值与实际值的差异的方式。它与二次代价函数相比更有效地促进ANN的训练。 在介绍交叉熵代价函数之前，我们需要了解二次代价函数的不足之处。二次代价函数的设计目的是使机器可以像人一样学习知识。但是，在实际应用中，二次代价函数存在一些缺陷。例如，在二类分类训练中，如果预测值与实际值的误差越大，参数调整的幅度可能更小，训练更缓慢。 交叉熵代价函数的公式推导可以分为以下步骤： 1. 首先，我们需要定义交叉熵代价函数的公式：H(y, y') = -∑[y log(y') + (1-y) log(1-y')] 其中，y是实际值，y'是预测值。 2. 然后，我们需要推导交叉熵代价函数的梯度：∂H/∂y' = -y/y' + (1-y)/(1-y') 3. 最后，我们可以使用梯度下降算法来最小化交叉熵代价函数。 交叉熵代价函数的优点是，它可以更好地衡量预测值与实际值的差异，从而使ANN的训练更加快速和准确。例如，在二类分类训练中，交叉熵代价函数可以使参数调整的幅度更大，训练更快收敛。 在实际应用中，交叉熵代价函数广泛应用于机器学习领域，例如图像分类、语音识别、自然语言处理等。它是ANN训练的核心组件之一，能够使ANN模型更加准确和可靠。 交叉熵代价函数是一种非常重要的机器学习技术，广泛应用于各种领域。它可以使ANN模型更加准确和可靠，提高机器学习的效率和效果。