被动调Q Nd³⁺:YAG 激光器的角锥棱镜研究
112 浏览量
更新于2024-08-29
收藏 316KB PDF 举报
"这篇文章是关于被动Q开关Nd^3+:YAG激光器的研究，其中使用了角锥反射镜。作者们分析了腔内偏振的变化，并通过数值模拟预测了随着角锥反射镜旋转角度变化时峰值功率、脉冲能量和脉冲宽度的改变。实验结果验证了理论分析，峰值功率的变化范围为1.77 MW，脉冲能量变化为14.9 mJ，脉冲宽度的波动为2.95 ns。"
这篇研究详细探讨了一种采用被动Q开关技术的Nd^3+:YAG激光器，该激光器中使用了角锥反射镜作为关键组件。Q开关是一种用于控制激光器输出脉冲能量和频率的技术，被动Q开关则是通过腔内的非线性光学效应实现这一目的，而非主动的电子或机械手段。在本研究中，角锥反射镜的旋转被用作调节激光性能的一种方法。
研究者首先对腔内偏振状态进行了理论分析，这是理解激光器工作模式的关键因素。他们利用数值模拟预测了当角锥反射镜绕其轴线旋转时，激光器的峰值功率、脉冲能量和脉冲宽度的动态变化。这种旋转可以改变激光腔内的光路，从而影响激光的振荡特性。
实验结果显示，角锥反射镜旋转带来的峰值功率变化相当显著，从10.36 MW降低到8.59 MW，变化范围达到了1.77 MW。同时，脉冲能量也发生了变化，从159.5 mJ增加到174.4 mJ，变动幅度为14.9 mJ。这表明角锥反射镜的角度调整能够有效地控制激光输出的能量特性。此外，脉冲宽度的波动为2.95 ns，尽管这个变化较小，但依然证明了角锥反射镜旋转对脉冲形状的影响。
实验结果与理论分析在变化规律上保持一致，验证了角锥反射镜作为调制手段的可行性。这种灵活的控制方式对于优化激光器的性能，特别是对于需要精确调整脉冲特性的应用，如激光加工、医疗设备和科学研究等领域，具有重要的实用价值。
这项工作展示了被动Q开关Nd^3+:YAG激光器设计的新思路，通过角锥反射镜的旋转实现对激光性能的精细调整，为激光技术的应用提供了新的可能性。
332 CHINESE OPTICS LETTERS / Vol. 4, No. 6 / June 10, 2006
Passively Q-switched Nd
3+
:YAG laser with corner cube
Weiqing Gao (
ppp
)
1
, Gongmin Yao (
õõõ
¬¬¬
)
1
, Lixin Xu (
NNN
ááá
###
)
1
,
Yong Cheng (
§§§
℄℄℄
)
2
, Hai Ming (
²²²
°°°
)
1
, and Jianping Xie (
ïïï
²²²
)
1
1
Department of Physics, University of Science and Technology of China, Hefei 230026
2
Optics Teaching and Research Room of Ordnance Noncommissioned Of f icer School, Wuhan 430064
Received January 9, 2006
A passively Q-switched Nd
3+
:YAG laser with corner cube is theoretically and experimentally studied. We
analyze the polarization variation in cavity and simulate the peak power, pulse energy and pulse width
changed with the rotation angle of corner cube numerically. An experiment is made to verify the theoretical
results. With rotating the angle of corner cube about the axis the variation range of peak power is 1.77 MW
(from 10.36 to 8.59 MW), and that of pulse energy is 14.9 mJ (from 159.5 to 174.4 mJ), the fluctuation
of pulse width is 2.95 ns. The experimental results agree with the theoretical analysis to the extent of
variation rules. The most dynamic to static energy ratio of 62.5% is achieved.
OCIS codes: 140.3540, 140.3580, 260.5430.
Because of low saturation intensity, high damaged
threshold, and excellent optical, chemical, and thermal
characteristics
[1]
, Cr
4+
:YAG can be used as passive Q -
switch in Nd
3+
:YAG laser
[2−6]
. Corner cube is insensitive
to vibration, impact, and great variety of temperature,
and can be used in adjust-free lasers
[7,8]
. The combina-
tion of Cr
4+
:YAG with corner cube will obtain adjust-free
Q-switched laser. Chun
[9]
and Singh
[10]
made use of the
crossed Porro prism to realize electro-optical Q-switched
laser. But this kind of resonant cavity is adjust-free only
in one dimension. Chen used corner cube as the resonant
cavity of passively Q-switched laser, and got the pulse
energy of 8.8 mJ and the peak power of 400 kW
[11]
. Shi-
mony et al. also realized passively Q-switched laser with
corner cube
[12]
. But none of them thought of the polar-
ization properties of corner cube, and the effects of the
polarization on the peak power, pulse energy, and pulse
width. We describe the polarization variation with the
rotation of corner cube about the axis in cavity
[13,14]
, and
simulate the peak power, pulse energy, and pulse width
changed with the rotation angle of corner cube numeri-
cally. An experiment is executed to verify the theoretical
results.
The polarization state of incident light will be changed
from linear polarization to elliptical polarization because
of the polarization properties of corner cube. When the
incident light comes to the bottom of corner cube ver-
tically, Liu et al. deduced the Jones matrix by vector
optics as
[15]
J
123
= R(−120
◦
) · T · R(60
◦
) · T · R(−60
◦
) · T · R(−60
◦
)
J
231
= R(120
◦
) · T · R(60
◦
) · T · R(−60
◦
) · T · R(180
◦
)
J
312
= R(0
◦
) · T · R(60
◦
) · T · R(−60
◦
) · T · R(60
◦
)
J
321
= R(−60
◦
) · T · R(−60
◦
) · T · R(60
◦
) · T · R(−120
◦
)
J
132
= R(180
◦
) · T · R(−60
◦
) · T · R(60
◦
) · T · R(120
◦
)
J
213
= R(60
◦
) · T · R(−60
◦
) · T · R(60
◦
) · T · R(0
◦
), (1)
where subscripts 123—213 are in correspondence with six
reflecting orders of incident light on three flanks of corner
cube. R(ε) =
cos ε sin ε
− sin ε cos ε
describes the coordinate
variation when light is reflected from one flank to an-
other. T =
r
p
0
0 r
s
is the variation of amplitude and
polarization between incident light and reflected light, r
p
and r
s
can be got from Fresnel formula.
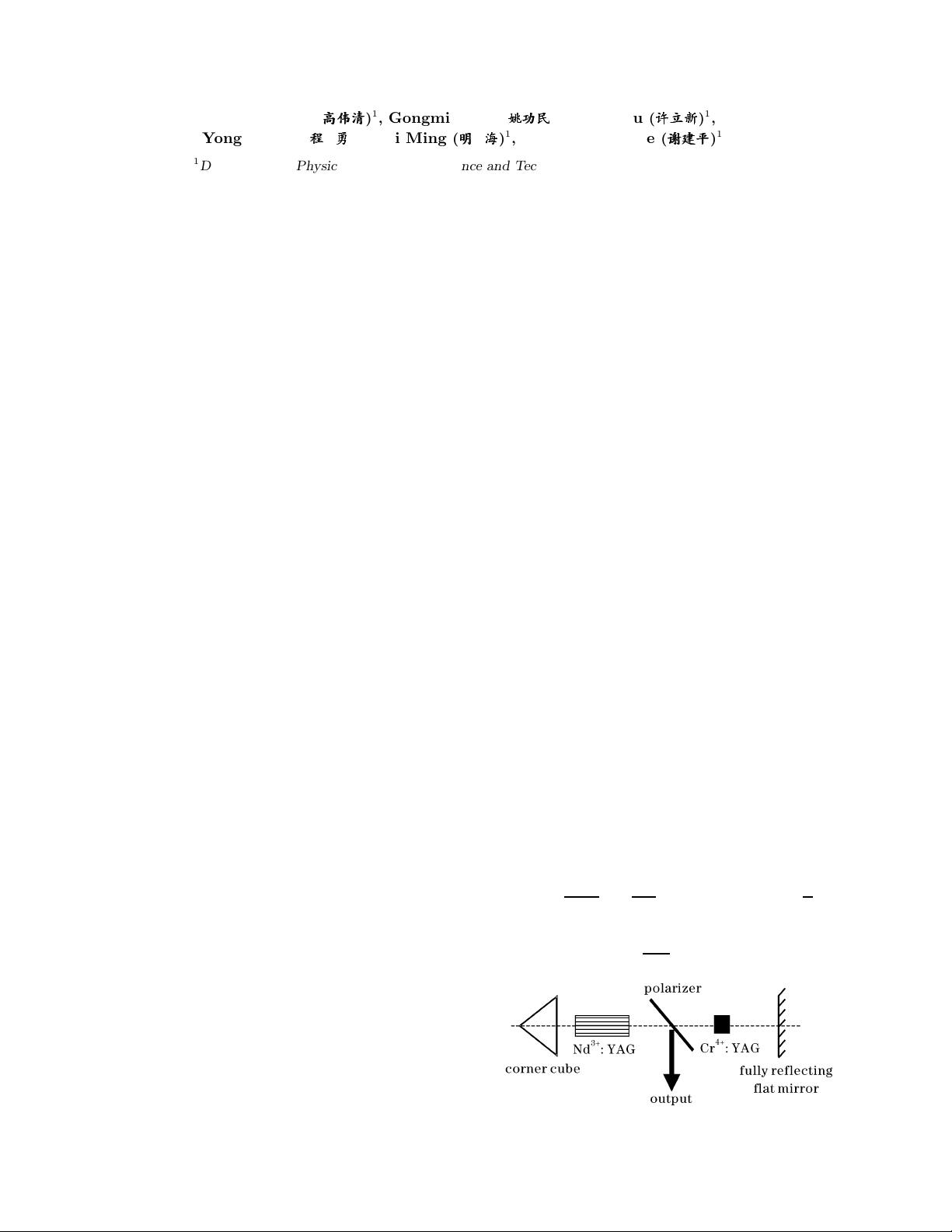
Our theoretical model is shown in Fig. 1. Resonant cav-
ity is formed by corner cube and fully reflecting flat mir-
ror. The gain material is Nd
3+
:YAG and the Q-switch is
Cr
4+
:YAG. The polarizer in the resonant cavity can pro-
vide the output beam of linear polarization. The cross
section of light beam in cavity is divided into six sym-
metric faculas (three pairs of conjugate faculas) because
of the diffraction of three edges of corner cube. Because
corner cube has the function of exchanging the situation
of light beam on space, the cavity is equivalent to three
sub-cavities. The three pairs of conjugate faculas enter
into Nd
3+
:YAG and Cr
4+
:YAG at different situations,
and pass through them four times each round trip (only
twice in flat-mirror cavity). This increases the gain of
cavity. Referring to the Refs. [16]—[18], we can deduce
the peak power and pulse energy of three sub-cavities as
P
m
(α) =
hνAl
γt
r
ln
1
R
m
(n
im
− n
tm
)
1 −
1
κ
× −n
t0m
ln
n
im
n
tm
, m = 1, 2, 3, (2)
Fig. 1. Theoretical model of passive Q-switched Nd
3+
:YAG
laser with corner cube.
1671-7694/2006/060332-04 http://www.col.org.cn
下载后可阅读完整内容，剩余3页未读，立即下载
2021-02-07 上传
2021-02-03 上传
2023-07-12 上传
2024-09-04 上传
2024-01-14 上传
2023-09-03 上传
2023-02-21 上传
2023-09-13 上传
2023-07-09 上传
weixin_38685831
- 粉丝: 8
- 资源: 874
我的内容管理
展开
最新资源
- JavaScript DOM事件处理实战示例
- 全新JDK 1.8.122版本安装包下载指南
- Python实现《点燃你温暖我》爱心代码指南
- 创新后轮驱动技术的电动三轮车介绍
- GPT系列：AI算法模型发展的终极方向？
- 3dsmax批量渲染技巧与VR5插件兼容性
- 3DsMAX破碎效果插件：打造逼真碎片动画
- 掌握最简GPT模型：Andrej Karpathy带你走进AI新时代
- 深入解析XGBOOST在回归预测中的应用
- 深度解析机器学习：原理、算法与应用
- 360智脑企业内测开启，探索人工智能新场景应用
- 3dsmax墙砖地砖插件应用与特性解析
- 微软GPT-4助力大模型指令微调与性能提升
- OpenSARUrban-1200：平衡类别数据集助力算法评估
- SQLAlchemy 1.4.39 版本特性分析与应用
- 高颜值简约个人简历模版分享
