L. Zou et al. / Digital Signal Processing 62 (2017) 125–136 127
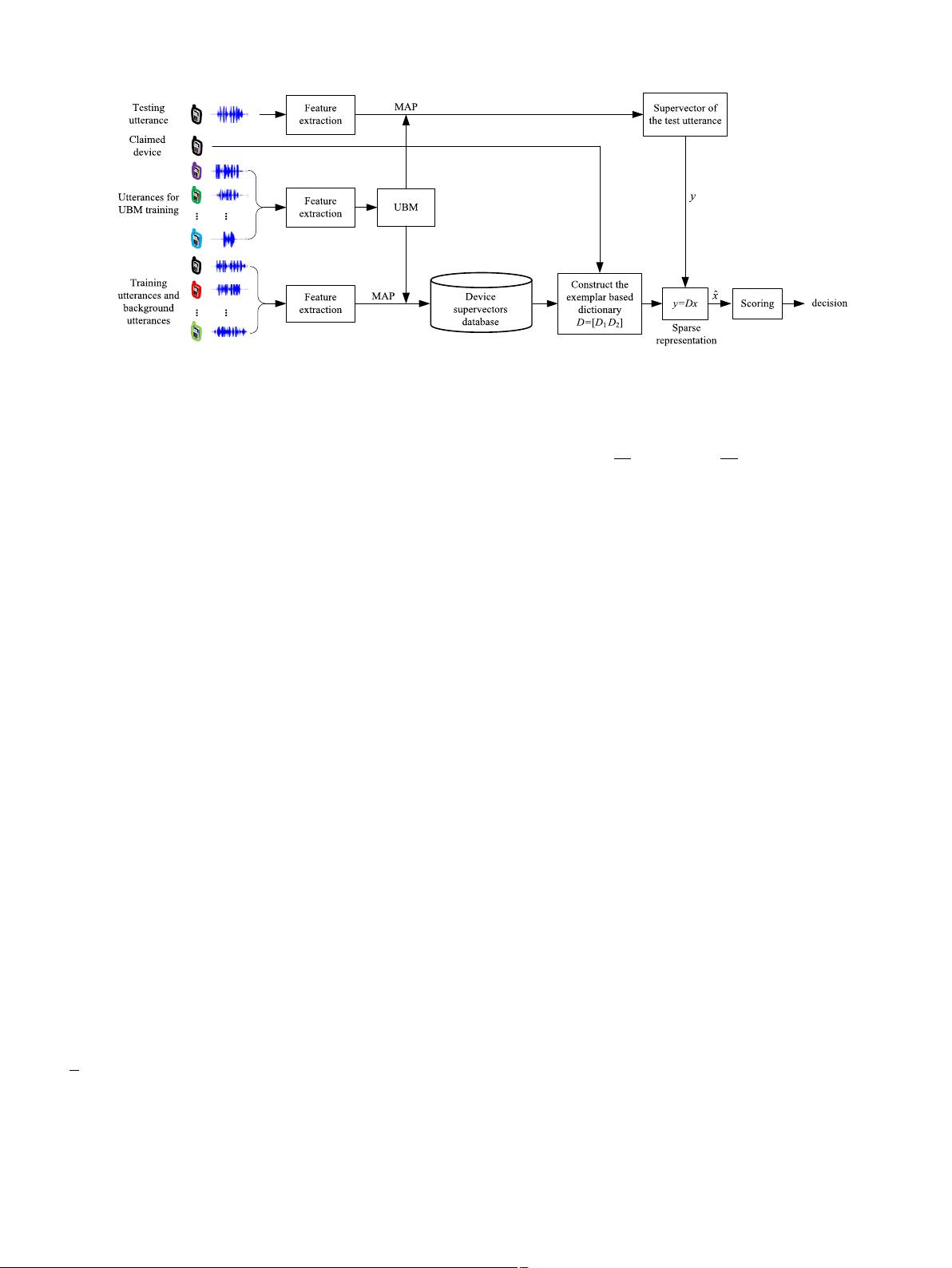
Fig. 1. Block diagram of source cell phone verification scheme based on sparse representation and exemplar dictionary.
show that the proposed scheme outperforms the exemplar dic-
tionary
based scheme, the unsupervised learned dictionary (here
K-SVD) based scheme and other two baseline methods. In addi-
tion,
we also analyze the influences of number of target examples
in exemplar dictionary and size of learned dictionary (by K-SVD)
on source cell phone verification performance.
The
rest of this paper is organized as follows. Section 2 de-
scribes
the method for extracting recording device intrinsic finger-
print.
Section 3 presents the sparse representation based source
cell phone verification schemes. Experimental setup and results
are provided in Section 4. Finally, conclusions and future work are
given in Section 5.
2. Recording device characterization
Over the last decade, various features were utilized to cap-
ture
the intrinsic characteristics of the recording devices. Gener-
ally
speaking, these features can be briefly grouped into three
categories: time domain, frequency domain and cepstral domain.
Specifically, mel-cepstral domain feature like MFCCs reported good
performance on source recording device recognition [26,27,44–46].
GSV, which is a high-dimensional vector (a.k.a. supervector) based
on low-dimensional feature vector (e.g., MFCCs), has been suc-
cessfully
applied to represent the intrinsic fingerprint of recording
device [26]. The signals in the speech recordings contain informa-
tion
not only related to recording device but also related to the
speech content such as speaker and linguistic information. It can
be deemed as the frequency response of the device contextual-
ized
by the speech content. GSV reduces the effects of the speech
content variability utilizing a statistical characterization of the fre-
quency
domain information of the contextualized signals.
The extraction procedure for GSV from a speech recording is
summarized as follows: Suppose that λ
UBM
={ω
i
, μ
i
,
i
}
M
i
=1
is a
diagonal covariance universal background model (UBM) with M
mixture
components, given a speech recording and the feature
vectors (here MFCCs) extracted from it, X ={x
t
}
T
t
=1
, the corre-
sponding
GMM is adapted from the UBM by adaptation of the
means through maximum a posteriori (MAP) [67,68]. More specif-
ically,
after computing the sufficient statistics for the weight and
mean parameters of mixture i as n
i
=
T
t
=1
P (i|x
t
) and E
i
(x) =
1
n
i
T
t
=1
P (i|x
t
)x
t
respectively, the ith adapted mean vector μ
i
is
computed as a weighted sum of the sufficient statistics for the
mean and the UBM mean: μ
i
= α
i
E
i
(x) + (1 − α
i
)μ
UBM
i
. Here,
α
i
is a data-dependent adaptation factor. It is defined as α
i
=
n
i
/(n
i
+ r) where r is a fixed relevance factor. Suppose that λ
a
=
{
ω
i
, μ
a
i
,
i
}
M
i
=1
and λ
b
={ω
i
, μ
b
i
,
i
}
M
i
=1
are the means adapted
GMMs corresponding to two speech recordings. The Kullback–
Leibler
(KL) divergence kernel is then defined as the corresponding
inner product of the GMM mean supervectors which is a concate-
nation
of the weighted GMM mean vectors [69]:
K (λ
a
,λ
b
) =
M
i=1
√
w
i
−1/2
i
μ
a
i
T
√
w
i
−1/2
i
μ
b
i
(1)
where M is the number of mixture components.
3. Cell phone verification by sparse representation
3.1. Scheme based on exemplar dictionary
We first present the exemplar dictionary based source cell
phone verification scheme. The corresponding block diagram is
shown in Fig. 1. During the verification process, for a claimed
device, N
1
target training examples (here GSV), represented as
{a
1i
}
N
1
i=1
, are placed together to construct D
1
=[a
11
, a
12
, ···, a
1N
1
] ∈
R
M×N
1
. At the same time, select N
2
non-target background exam-
ples,
represented as {a
2i
}
N
2
i=1
, from the background supervectors to
construct D
2
=[a
21
, a
22
, ···, a
2N
2
] ∈ R
M×N
2
and satisfy N
1
N
2
.
Thus, the exemplar dictionary is constructed by incorporating D
1
and D
2
as
D =[D
1
D
2
]
=[
a
11
, a
12
, ···,a
1N
1
, a
21
, a
22
, ···,a
2N
2
]∈R
M×N
(2)
where N = N
1
+ N
2
. Note that M < N should be satisfied for ob-
taining
a redundant and overcomplete dictionary. The atoms in
dictionary D are normalized to unit
2
-norm as in [55]. Then, given
a test vector y ∈ R
M
with unit
2
-norm and suppose that y can be
linearly represented with respect to D as
y = Dx =[D
1
D
2
]
x
1
x
2
(3)
where x is the coefficient vector. Fig. 2 shows an example of sparse
coefficient vectors for target and non-target trial. If y belongs to a
valid test, i.e., it comes from a speech recording recorded by the
claimed device, it will approximately lie in the linear span of the
columns of D
1
. Thus, the non-zero entries of coefficient vector x
associated
with D
1
(i.e., x
1
) will be large compared to the non-zero
entries of coefficient vector x associated with D
2
(i.e., x
2
) as shown
in Fig. 2(a). On the other hand, if y belongs to an invalid test, i.e.,
it comes from a speech recording, which is not recorded by the
claimed device, the coefficient vectors will be sparsely distributed
across D
1
and D
2
as shown in Fig. 2(b). The sparse solution to
(3) can be obtained by solving the following optimization problem
[66]:









