物联网控制实验：传递函数与结构图建模

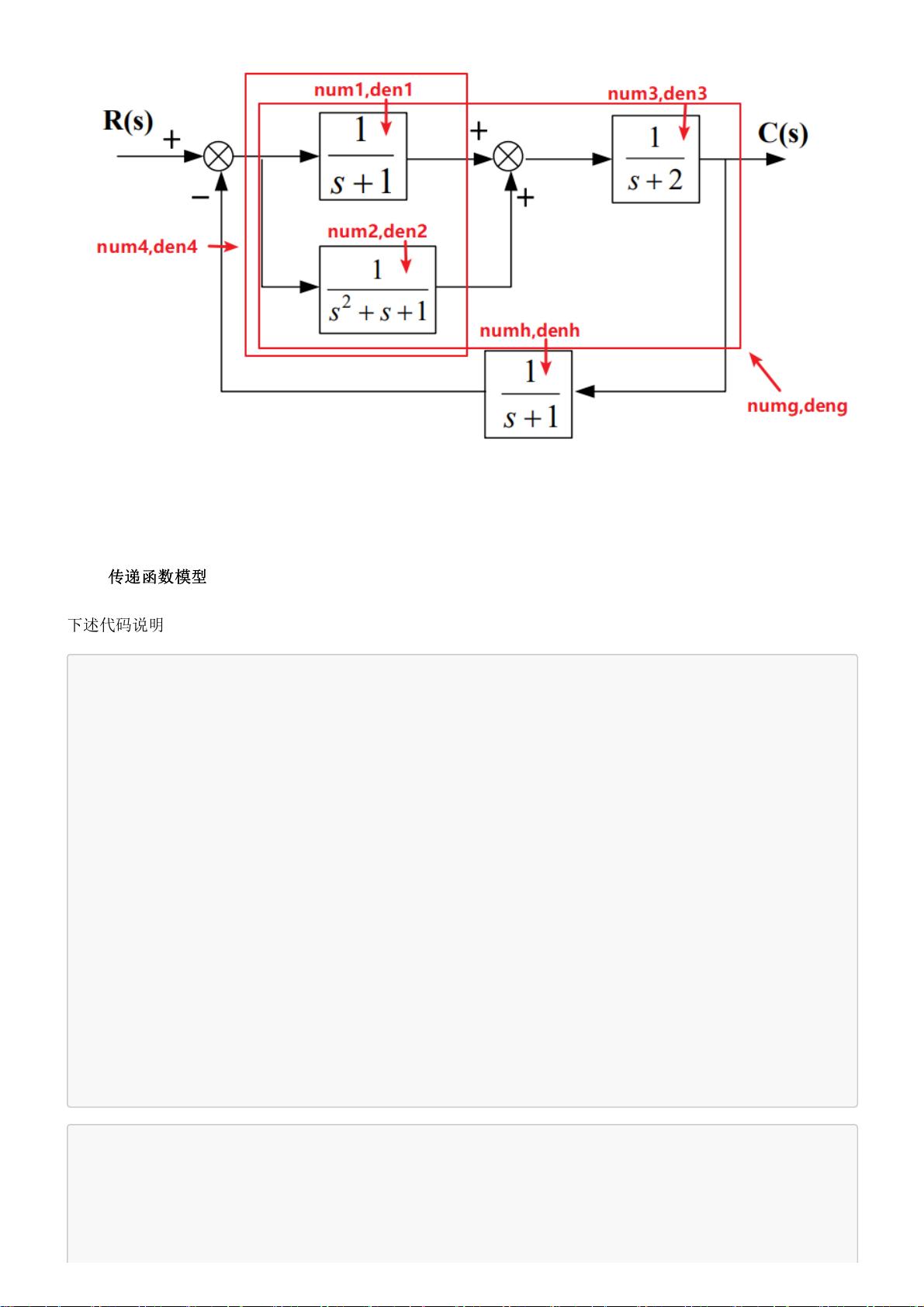
本资源是一份关于物联网控制实验的笔记，主要介绍了MATLAB中用于分析和设计线性定常系统的数学模型。笔记分为两个主要部分： 1. 常用数学模型： - 传递函数模型：传递函数是描述线性定常系统动态特性的一种基本方法，它表示输入信号与输出信号之间的关系。在MATLAB中，传递函数由分子多项式num和分母多项式den组成，如`sys=tf(num,den)`。分子多项式按s的降幂排列，如`[b1,b2,...,bm,bm+1]`，分母多项式同理。通过函数`tf2zp()`可以将传递函数转换为零极点增益模型，`zp2tf()`则反之。 - 零极点增益模型：该模型表示系统增益K、零点zi和极点pj的集合，用`[z,p,K]`的形式表示。例如，`sys1=zpk(sys)`将传递函数转换为零极点形式。 - 部分分式展开：函数`residue()`用于对传递函数的比进行部分分式展开，有助于理解和设计复杂的控制系统。 2. 控制系统结构图模型： - 串联连接：两个或多个环节G1(s)和G2(s)通过串联方式组合，`[num,den]=series(num1,den1,num2,den2)`计算串联后的传递函数。 - 并联连接：系统通过并联连接时，多个环节的传递函数相加，`[num,den]=parallel(num1,den1,num2,den2)`。 - 反馈：闭环控制系统中，常用`cloop()`和`feedback()`函数来处理反馈信号。`cloop()`函数适用于单位反馈情况，`[num,den]=cloop(numg,deng,sign)`用于计算闭环传递函数。 这些内容对于理解和设计基于MATLAB的物联网控制系统至关重要，包括系统建模、分析其动态性能以及实现不同的系统结构。通过熟练运用这些工具和概念，可以有效地解决实际工程中的控制问题。