机器学习驱动的电子设计自动化综述：进展与挑战

需积分: 10 144 浏览量更新于2024-07-15 收藏 3.48MB PDF 举报

随着CMOS技术的缩小，大规模集成电路（VLSI）的设计复杂性呈现出显著增长。自20世纪90年代起，机器学习（Machine Learning, ML）技术在电子设计自动化（Electronic Design Automation, EDA）领域的应用就已萌芽，但近期ML技术的突破和EDA任务的日益复杂，使得人们对其在解决ED设计问题上的潜力产生了更大的兴趣。本篇综述论文由清华大学的汪玉等人撰写，涵盖了中国香港科技大学的研究团队，共同探讨了ML在EDA中的应用。该研究旨在提供一个全面的ML在EDA领域的回顾，按照EDA流程的层级结构进行组织。EDA是一个广泛的领域，主要包括功能设计、综合、验证、物理设计（包括布局、布线、版图设计规则检查等）。在这个框架下，论文作者回顾了历史上的ML应用案例，重点关注了神经网络等机器学习模型在各个环节的潜在贡献与挑战。机器学习在EDA中的应用可以分为以下几个方面： 1. **功能设计**：ML可以通过模式识别和预测分析帮助设计者优化电路行为，提升设计效率，尤其是在处理大规模数据集和复杂系统时。 2. **综合**：通过自动化工具，ML可以学习电路拓扑结构和约束条件，以减少手工干预，实现更高效的电路整合。 3. **验证**：ML技术可用于自动检测电路设计中的错误，提高验证的准确性和速度，减少设计迭代周期。 4. **物理设计**：布局和布线是EDA中的关键步骤，ML能支持智能路径规划、优化布局策略，甚至通过生成对抗网络（GANs）改进版图质量。 5. **设计规则检查**：ML可以协助制定更精确的设计规则，确保设计满足工艺规格，并通过模式识别快速定位和修复违规问题。值得注意的是，论文还提到了一些额外的关键词和短语，如“电子设计自动化”、“机器学习”以及“神经网络”，这些关键词反映了文章的核心关注点。整体而言，这篇综述论文不仅梳理了ML在EDA中的历史进展，还展望了未来可能的发展趋势和面临的挑战，为研究人员和工程师提供了宝贵的参考资源。

x:8 G. Huang et al.

Initial Training

Initial Samples

ML Predictor

training

Active Learning

ML Predictor

Predicting results

for all design points

Refinement

samples

training

Explorer /

Sampler

Fig. 4. The iterative-refinement DSE framework (reproduced from [93]).

Pareto Frontier Curve, on which every point is not fully dominated by any other points under all

the metrics.

Classical search algorithms have been applied in HLS DSE, such as Simulated Annealing (SA) and

Genetic Algorithm (GA). But these algorithms are unable to learn from the database of previously

explored designs. Many previous studies use an ML predictive model to guide the DSE. The models

are trained on the synthesis results of explored design points, and used to predict the quality of

new designs (See more discussions on this active learning workow in Section 9.1). Typical studies

are elaborated in Section 3.2.1. There is also a thread of work that involves learning-based methods

to improve the inecient or sensitive part of the classical search algorithms, as elaborated in

Section 3.2.2. Some work included in this subsection focuses on system-level DSE rather than HLS

design [74], or general active learning theories [177].

3.2.1 Active Learning. The four papers visited in this part utilize the active learning approach to

perform DSE for HLS, and use predictive ML models to surrogate actual synthesis when evaluating

a design. Liu and Schäfer

[92]

propose a design space explorer which selects new designs to

implement through an active learning approach. Transductive Experimental Design (TED) [

]

focuses on seeking the samples that describes the design space accurately. Pareto Active learning

(PAL) [

177

] proposed an active learning algorithm that samples the design which the learner

cannot clearly classify. Instead of focusing on how accurately the model describes the design space,

Adaptive Threshold Non-Pareto Elimination (ATNE) [

109

] estimates the inaccuracy of the learner

and achieves better performance than TED and PAL.

Liu and Schäfer

[92]

propose a dedicated explorer to search for Pareto-optimal HLS designs for

FPGAs. The explorer iteratively selects potential Pareto-optimal designs to synthesize and verify.

The selection is based on a set of important features, which are adjusted during the exploration. The

proposed method runs 6.5

faster than an exhaustive search, and runs 3.0

faster than a restricted

search method but nds results with higher quality.

The basic idea of TED [

] is to select representative as well as the hard-to-predict samples from

the design space, instead of the random sample used in previous work. The target is to maximize

the accuracy of the predictive model with the fewest training samples. The authors formulate the

problem of nding the best sampling strategy as follows: TED assumes that the overall number

of knob settings is

𝑛

(

|K | = 𝑛

), from which we want to select a training set

such that

K| = 𝑚

Minimizing the prediction error

𝐻 (𝑘) −

𝐻 (𝑘)

for all

𝑘 ∈ K

is equivalent to the following problem:

𝑚𝑎𝑥

𝑇 [K

𝑇

(

𝑇

+ 𝜇𝐼 )

−1

] 𝑠.𝑡 .

K ⊂ K, |

K| = 𝑚,

ACM Trans. Des. Autom. Electron. Syst., Vol. x, No. x, Article x. Publication date: January 0000.

Machine Learning for Electronic Design Automation: A Survey x:9

SA/GA-Based

Design Space

Explorer

Local Search

ML Predictor

Meta Search

New search trajectory to

improve the predictor

Good starting states to find

better designs

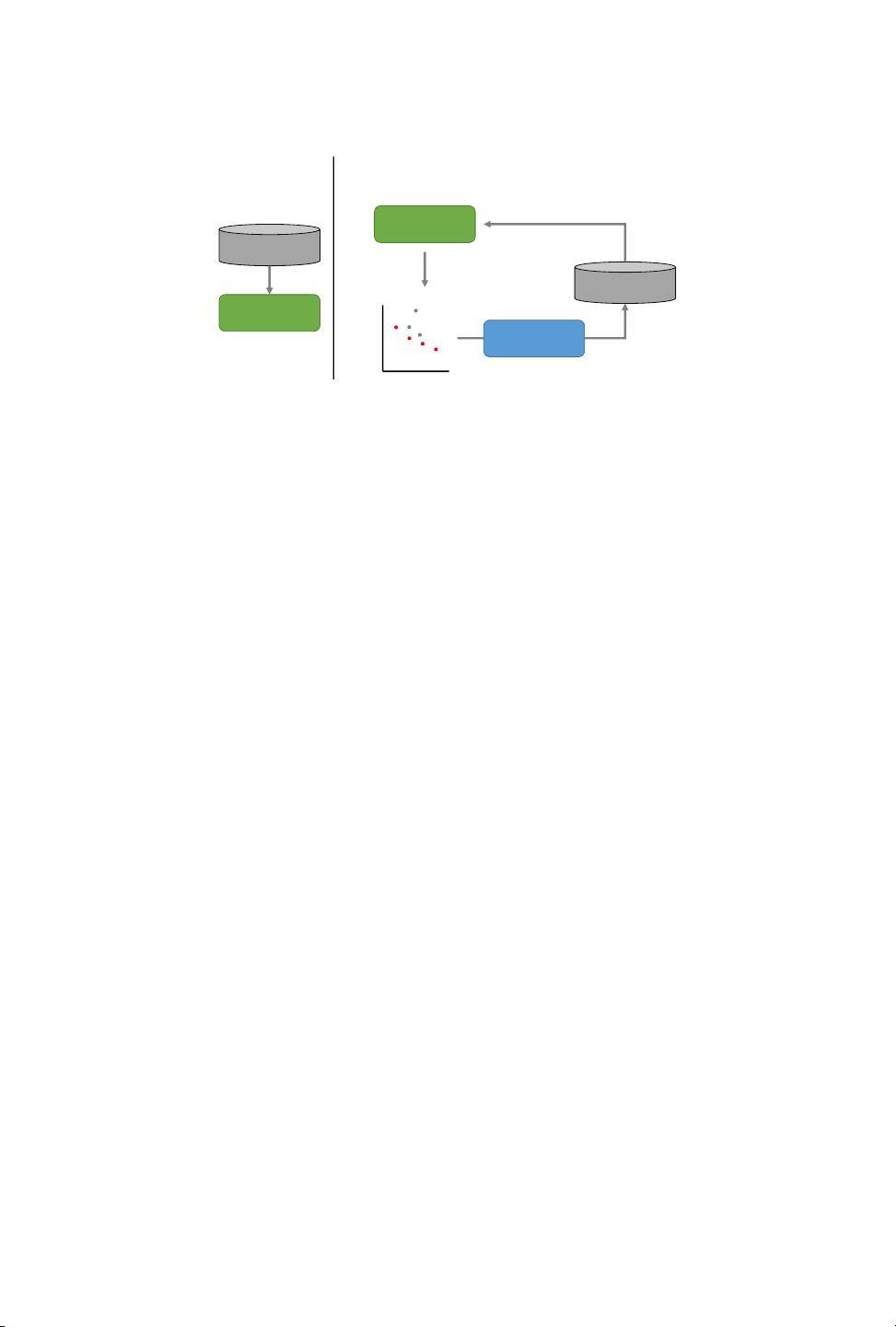
Fig. 5. Overview of the STAGE algorithm (reproduced from [74]).

where

𝑇 [·]

is the matrix trace operator and

𝜇 > 0

. The authors interprete their solution as sampling

from a set

K that span a linear space, to retain most of the information of K [93].

PAL [

177

] is proposed for general active learning scenarios, and is demonstrated by a sorting

network synthesis DSE problem in the paper. It uses Gaussian Process (GP) to predict Pareto-

optimal points in design space . The models predict the objective functions to identify points that

are Pareto-optimal with high probabilities. A point

𝑥

that has not been sampled is predicted as

𝑓 (𝑥) = 𝜇 (𝑥)

and

𝜎 (𝑥)

is interpreted as the uncertainty of the prediction which can be captured by

the hyperrectangle

𝑄

𝜇,𝜎,𝛽

(𝑥) =

𝑦 : 𝜇 (𝑥) − 𝛽

1/2

𝜎 (𝑥) ⪯ 𝑦 ⪯ 𝜇 (𝑥) + 𝛽

1/2

𝜎 (𝑥)

where

𝛽

is a scaling parameter to be chosen. PAL focuses on accurately predicting points near the

Pareto frontier, instead of the whole design space. In every iteration, the algorithm classies samples

into three groups: Pareto-optimal, Non-Pareto-optimal, and uncertain ones. The next design point

to evaluate is the one with the largest uncertainty, which intuitively has more information to

improve the model. The training process is terminated when there are no uncertain points. The

points classied as Pareto-optimal are then returned.

ATNE [

109

] utilizes Random Forest (RF) to aid the DSE process. This work uses a Pareto iden-

tication threshold that adapts to the estimated inaccuracy of the RF regressor and eliminates

the non-Pareto-optimal designs incrementally. Instead of focusing on improving the accuracy of

the learner, ATNE focuses on estimating and minimizing the risk of losing “good” designs due to

learning inaccuracy.

3.2.2 Machine Learning for Improving Other Optimization Algorithms. In this part, we summarize

three studies that use ML techniques to improve classical optimization algorithms.

STAGE [

] is proposed for DSE of many-core systems. The motivating observation of STAGE is

that the performance of simulated annealing is highly sensitive to the starting point of the search

process. The authors build an ML model to learn which parts of the design space should be focused

on, eliminating the times of futile exploration [

]. The proposed strategy is divided into two stages.

The rst stage (local search) performs a normal local search, guided by a cost function based on the

designer’s goals. The second stage (meta search) tries to use the search trajectories from previous

local search runs to learn to predict the outcome of local search given a certain starting point [

Fast Simulated Annealing (FSA) [

104

] utilizes the decision tree to improve the performance of

SA. Decision tree learning is a widely used method for inductive inference. The HLS pragmas are

taken as input features. FSA rst performs standard SA to generate enough training sets to build

ACM Trans. Des. Autom. Electron. Syst., Vol. x, No. x, Article x. Publication date: January 0000.

剩余43页未读，继续阅读

syp_net

粉丝: 158
资源: 1187

机器学习驱动的电子设计自动化综述：进展与挑战

自动化学院网站设计毕业论文.docx

SVM（包括LS-SVM）相关入门论文by 清华大学自动化系张学工（2）

清华大学崔鹏等最新「分布外泛化(Out-Of-Distribution Generalization)」 综述论文

清华最新《图神经网络推荐系统》综述论文

清华电力系统调度自动化15配电自动化.pptx

usb接口设计（清华大学毕业设计论文 )

usb接口设计（清华大学毕业设计论文 ）

清华自动化系网络课件

清华大学自动化系小学期“现代电子系统设计”课程综创实验源码与报告——基于PSoC6的多功能平衡车.zip

清华&南开最新「视觉注意力机制Attention」综述论文

最新资源

清华大学崔鹏等最新「分布外泛化(Out-Of-Distribution Generalization)」综述论文

usb接口设计（清华大学毕业设计论文）