图论基础与应用：从七桥问题到最短路径算法

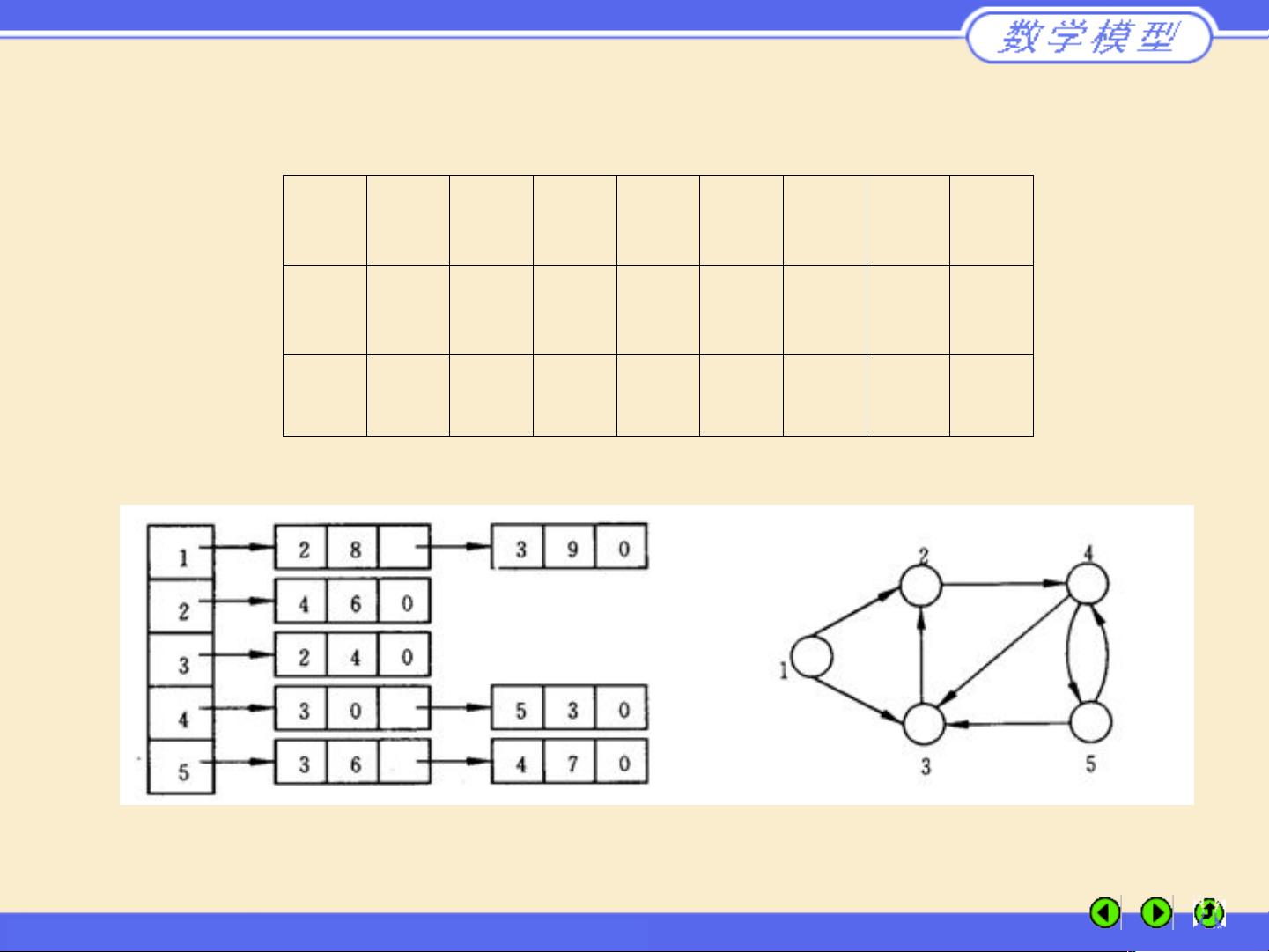
图论是数学的一个分支，主要研究的是由顶点和边构成的结构，它在众多领域中有着广泛的应用，包括物理、化学、通信科学、建筑学、生物遗传学、心理学、经济学和社会学等。图论的起源可以追溯到1736年的“哥尼斯堡的七座桥”问题，这个问题促使人们开始用图形的方式思考连通性问题。随后，克希霍夫在电网络研究中引入了“树”概念，凯莱在分析烷烃分子的同分异构体时也发现了树的概念。 图论的基本概念包括图(graph)、有向图(directed graph)和无向图(undirected graph)等。顶点(vertex)和边(edge)是构成图的基本元素，度(degree)描述了每个顶点与其他顶点相连的边的数量。权(weight)则用于赋予边特定的数值，如距离或成本。路径(path)是连接顶点的一系列边，有向图和无向图在表示路径时有所不同。 图的表示方法有多种，如邻接矩阵、关联矩阵、边列表、正向表、逆向表和邻接表。邻接矩阵是一种二维数组，其中的元素表示顶点间是否有边以及边的权重；关联矩阵则是根据边的顺序列出的信息；边列表则按顺序列出图中所有的边；正向表和逆向表是针对有向图的，记录了从一个顶点出发的所有边；邻接表则更高效地存储无向图的边信息，只包含起点和终点的连接。 与图论相关的具体问题包括： 1. **最短路问题** (SPP)：寻找两个顶点之间的最短路径，如迪克斯特拉(Dijkstra)算法就是解决此类问题的经典方法。在示例中，公司间的航班票价矩阵就是一个最短路径问题实例，通过编程求解可以找到从第一个城市到其他城市的最短航线。 2. **公路连接问题**：涉及如何优化交通网络的布局，以达到最低成本或最小时间的连通性。 3. **指派问题** (Assignment Problem)：分配任务或资源给不同的对象，使得总成本或效率达到最优。 4. **中国邮递员问题** (CPP)：经典的旅行商问题变种，涉及邮政员如何访问所有城市并返回起点，使总路程最短。 5. **旅行商问题** (TSP)：旅行商问题的核心挑战，即找到一条最短路径，使得旅行商能访问所有城市且只访问一次。 6. **运输问题** (Transportation Problem)：涉及分配货物或资源，使得运输成本最低，同时满足需求。 理解并掌握这些基本概念和问题对于从事计算机科学、工程、数学和应用领域的专业人士来说至关重要，因为它们在实际项目中扮演着关键的角色。通过学习图论，不仅可以解决实际问题，还能增强逻辑思维和抽象能力。