深度学习入门：神经网络与实践

5星 · 超过95%的资源 | 下载需积分: 50 | PDF格式 | 5.69MB | 更新于2024-07-16 | 39 浏览量 | 举报

"《神经网络与深度学习》是一本深入浅出的深度学习入门书籍，由Michael Nielsen撰写，英文原版可在[1]网址获取。本书结合理论与实践，旨在帮助读者理解和掌握神经网络的基础概念和实际应用，特别是针对手写数字识别这一经典问题进行讲解。第1章介绍了如何使用神经网络来识别手写数字。首先，作者通过Perceptron模型（感知机）概述了基本的逻辑单元，然后引入了Sigmoid神经元，强调其在处理非线性问题上的优势。接着，书中详细讨论了神经网络的架构，包括多层网络设计，以及如何构建一个简单的网络来对MNIST数据集中的手写数字进行分类。学习过程的核心是梯度下降法，该方法展示了如何调整权重以最小化预测误差。第2章着重于反向传播算法，这是训练深层神经网络的关键技术。作者首先用矩阵运算演示了一个简化的神经网络输出计算，然后揭示了成本函数的两个关键假设。Hadamard乘法在此过程中扮演重要角色，推动理解四条基础方程。这部分还提供了这些方程的证明，并给出了完整的反向传播算法步骤，以及为何它被视为一种高效的计算策略。此外，作者还探讨了反向传播的大局观，即它如何在整个网络中传递误差信号。第3章聚焦于改进神经网络的学习方式。这里涉及了如何优化网络结构、正则化方法、以及防止过拟合的策略。作者可能会介绍不同类型的损失函数，如交叉熵损失，以及批量归一化和Dropout等常用技术，以提升模型性能和泛化能力。《神经网络与深度学习》提供了一个循序渐进的学习路径，从基础知识到核心算法，再到实践技巧，让读者逐步建立起深度学习的基础，并能够在实践中构建和优化自己的神经网络模型。无论是对于初学者还是希望深入了解深度学习的工程师，这本书都是一份宝贵的资源。"

展开



Using neural nets to recognize handwritten digits

very complicated way. So while your “9” might now be classiﬁed correctly, the behaviour of

the network on all the other images is likely to have completely changed in some hard-to-

control way. That makes it difﬁcult to see how to gradually modify the weights and biases so

that the network gets closer to the desired behaviour. Perhaps there’s some clever way of

getting around this problem. But it’s not immediately obvious how we can get a network of

perceptrons to learn.

We can overcome this problem by introducing a new type of artiﬁcial neuron called a

sigmoid neuron. Sigmoid neurons are similar to perceptrons, but modiﬁed so that small

changes in their weights and bias cause only a small change in their output. That’s the crucial

fact which will allow a network of sigmoid neurons to learn.

Okay, let me describe the sigmoid neuron. We’ll depict sigmoid neurons in the same way

we depicted perceptrons:

Just like a perceptron, the sigmoid neuron has inputs,

, x

,...

. But instead of being just 0

or 1, these inputs can also take on any values between 0 and 1. So, for instance, 0

638

...

is a

valid input for a sigmoid neuron. Also just like a perceptron, the sigmoid neuron has weights

for each input,

, w

,...

, and an overall bias,

. But the output is not 0 or 1. Instead, it’s

σ(wx + b), where σ is called the sigmoid function

, and is deﬁned by:

σ(z) ≡

1 + e

−z

. (1.3)

To put it all a little more explicitly, the output of a sigmoid neuron with inputs

...

weights w

, w

,..., and bias b is

1 + exp



−

− b



. (1.4)

At ﬁrst sight, sigmoid neurons appear very different to perceptrons. The algebraic form of

the sigmoid function may seem opaque and forbidding if you’re not already familiar with

it. In fact, there are many similarities between perceptrons and sigmoid neurons, and the

algebraic form of the sigmoid function turns out to be more of a technical detail than a true

barrier to understanding.

To understand the similarity to the perceptron model, suppose

z ≡ w · x

is a large

positive number. Then

−z

≈

0 and so

(

)

≈

1. In other words, when

w · x

is large

and positive, the output from the sigmoid neuron is approximately 1, just as it would have

been for a perceptron. Suppose on the other hand that

w · x

is very negative. Then

−z

→ ∞

, and

(

)

≈

0. So when

w · x

is very negative, the behaviour of a sigmoid

Incidentally,

is sometimes called the logistic function, and this new class of neurons called logistic

neurons. It’s useful to remember this terminology, since these terms are used by many people working

with neural nets. However, we’ll stick with the sigmoid terminology.



Using neural nets to recognize handwritten digits

where the sum is over all the weights,

, and

∂ output/∂ w

and

∂ output/∂ b

denote partial

derivatives of the output with respect to

and

, respectively. Don’t panic if you’re not

comfortable with partial derivatives! While the expression above looks complicated, with all

the partial derivatives, it’s actually saying something very simple (and which is very good

news):

∆output

is a linear function of the changes

∆w

and

∆b

in the weights and bias.

This linearity makes it easy to choose small changes in the weights and biases to achieve

any desired small change in the output. So while sigmoid neurons have much of the same

qualitative behavior as perceptrons, they make it much easier to ﬁgure out how changing

the weights and biases will change the output.

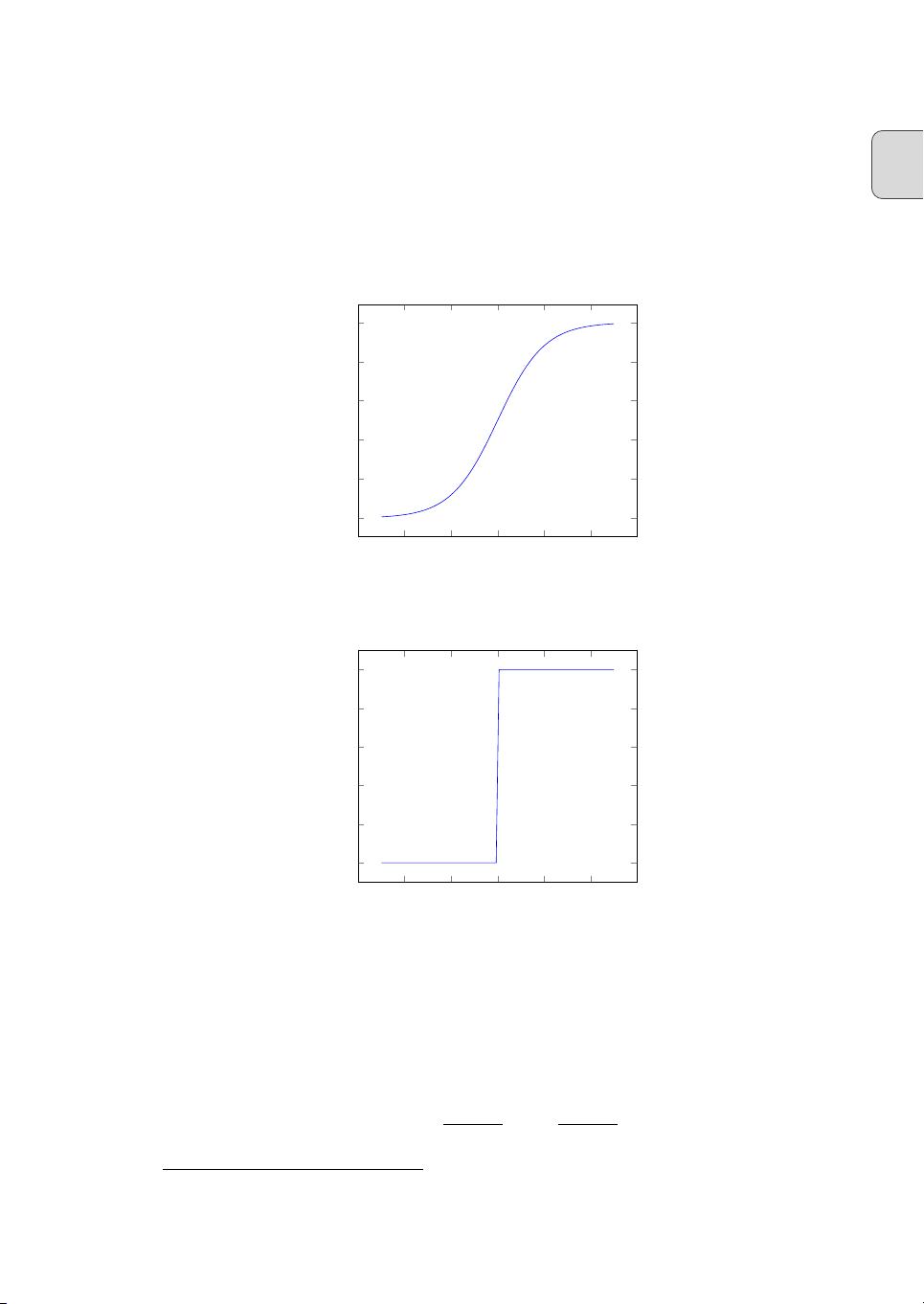
If it’s the shape of

which really matters, and not its exact form, then why use the

particular form used for

in Equation 1.3? In fact, later in the book we will occasionally

consider neurons where the output is

(

w·x

) for some other activation function

(

). The

main thing that changes when we use a different activation function is that the particular

values for the partial derivatives in Equation 1.5 change. It turns out that when we compute

those partial derivatives later, using

will simplify the algebra, simply because exponentials

have lovely properties when differentiated. In any case,

is commonly-used in work on

neural nets, and is the activation function we’ll use most often in this book.

How should we interpret the output from a sigmoid neuron? Obviously, one big difference

between perceptrons and sigmoid neurons is that sigmoid neurons don’t just output 0 or

1. They can have as output any real number between 0 and 1, so values such as 0.173

...

and 0.689

...

are legitimate outputs. This can be useful, for example, if we want to use the

output value to represent the average intensity of the pixels in an image input to a neural

network. But sometimes it can be a nuisance. Suppose we want the output from the network

to indicate either “the input image is a 9” or “the input image is not a 9”. Obviously, it’d be

easiest to do this if the output was a 0 or a 1, as in a perceptron. But in practice we can

set up a convention to deal with this, for example, by deciding to interpret any output of at

least 0.5 as indicating a “9”, and any output less than 0.5 as indicating “not a 9”. I’ll always

explicitly state when we’re using such a convention, so it shouldn’t cause any confusion.

Exercises

• Sigmoid neurons simulating perceptrons, part I

Suppose we take all the weights

and biases in a network of perceptrons, and multiply them by a positive constant, c>0.

Show that the behavior of the network doesn’t change.

• Sigmoid neurons simulating perceptrons, part II

Suppose we have the same setup

as the last problem – a network of perceptrons. Suppose also that the overall input to

the network of perceptrons has been chosen. We won’t need the actual input value, we

just need the input to have been ﬁxed. Suppose the weights and biases are such that

w · x

b 6

= 0 for the input x to any particular perceptron in the network. Now replace

all the perceptrons in the network by sigmoid neurons, and multiply the weights and

biases by a positive constant

c >

0. Show that in the limit as

c → ∞

the behaviour of

this network of sigmoid neurons is exactly the same as the network of perceptrons.

How can this fail when w · x + b = 0 for one of the perceptrons?

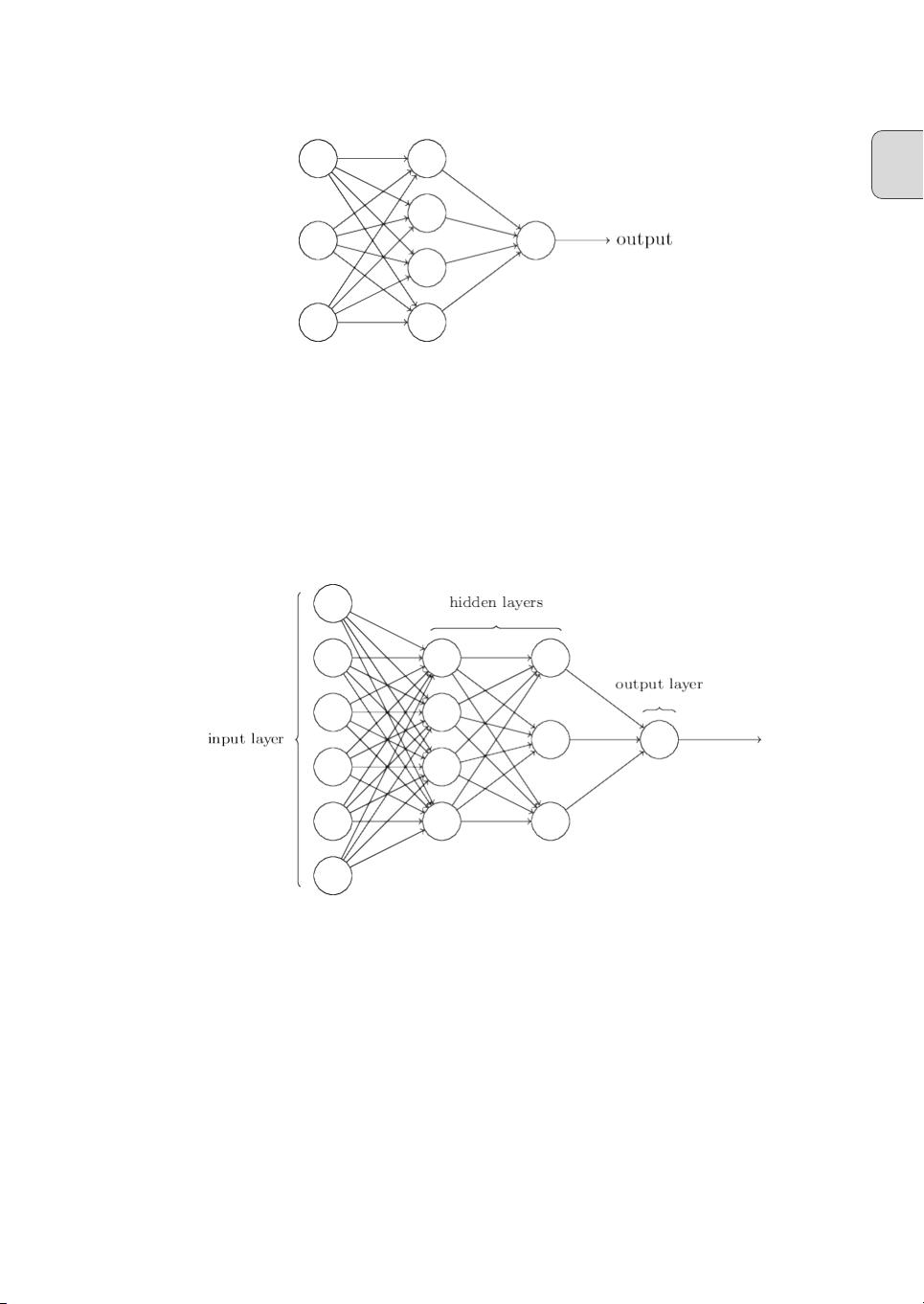
1.3 The architecture of neural networks

In the next section I’ll introduce a neural network that can do a pretty good job classifying

handwritten digits. In preparation for that, it helps to explain some terminology that lets us

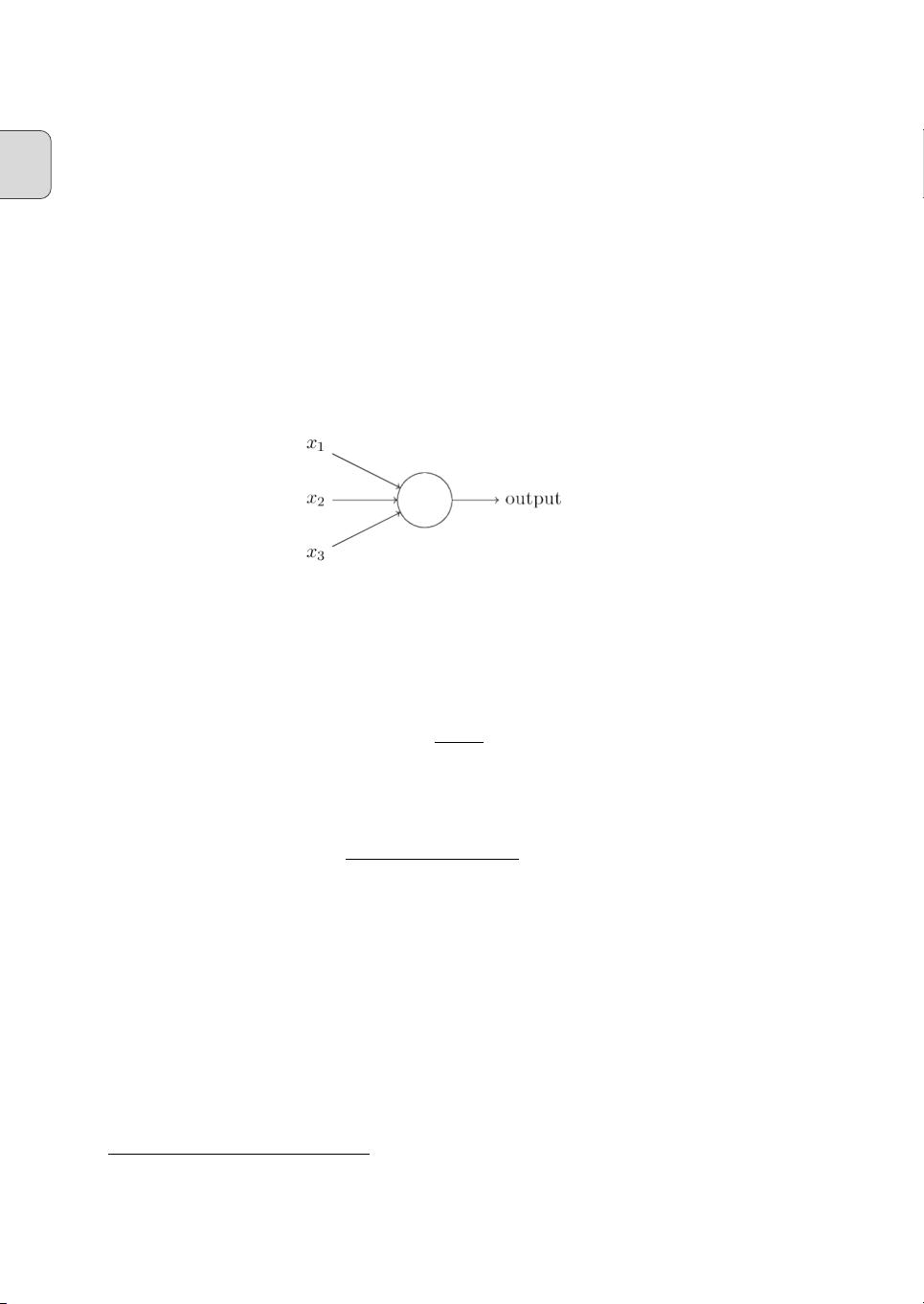
name different parts of a network. Suppose we have the network:



Using neural nets to recognize handwritten digits

possible to sum up the design process for the hidden layers with a few simple rules of thumb.

Instead, neural networks researchers have developed many design heuristics for the hidden

layers, which help people get the behaviour they want out of their nets. For example, such

heuristics can be used to help determine how to trade off the number of hidden layers against

the time required to train the network. We’ll meet several such design heuristics later in this

book.

Up to now, we’ve been discussing neural networks where the output from one layer is

used as input to the next layer. Such networks are called feedforward neural networks. This

means there are no loops in the network – information is always fed forward, never fed

back. If we did have loops, we’d end up with situations where the input to the

function

depended on the output. That’d be hard to make sense of, and so we don’t allow such loops.

However, there are other models of artiﬁcial neural networks in which feedback loops

are possible. These models are called recurrent neural networks. The idea in these models is

to have neurons which ﬁre for some limited duration of time, before becoming quiescent.

That ﬁring can stimulate other neurons, which may ﬁre a little while later, also for a limited

duration. That causes still more neurons to ﬁre, and so over time we get a cascade of neurons

ﬁring. Loops don’t cause problems in such a model, since a neuron’s output only affects its

input at some later time, not instantaneously.

Recurrent neural nets have been less inﬂuential than feedforward networks, in part

because the learning algorithms for recurrent nets are (at least to date) less powerful. But

recurrent networks are still extremely interesting. They’re much closer in spirit to how our

brains work than feedforward networks. And it’s possible that recurrent networks can solve

important problems which can only be solved with great difﬁculty by feedforward networks.

However, to limit our scope, in this book we’re going to concentrate on the more widely-used

feedforward networks.

1.4 A simple network to classify handwritten digits

Having deﬁned neural networks, let’s return to handwriting recognition. We can split the

problem of recognizing handwritten digits into two sub-problems. First, we’d like a way

of breaking an image containing many digits into a sequence of separate images, each

containing a single digit. For example, we’d like to break the image

into six separate images,

We humans solve this segmentation problem with ease, but it’s challenging for a computer

program to correctly break up the image. Once the image has been segmented, the program

then needs to classify each individual digit. So, for instance, we’d like our program to

recognize that the ﬁrst digit above,

剩余223页未读，继续阅读

身份认证购VIP最低享 7 折!

30元优惠券

四道眉毛

粉丝: 4

深度学习入门：神经网络与实践

Neural Networks and Deep Learning中文版

Neural Networks and Deep Learning.神经网络与深度学习

《Neural Networks and Deep Learning》（美）Michael Nielsen 著 英文版.pdf

吴恩达系列教学码源 Neural Networks and Deep Learning.zip

Neural Networks and Deep Learning A Textbook 完整版

neural networks and deep learning --michael nielsen

Neural Networks and Deep Learning 笔记及课后习题

Neural Networks and Deep Learning

Neural Networks and Deep Learning - 神经网络与深度学习 中英双版本

神经网络和深度学习neural networks and deep-learning-zh.pdf

最新资源

《Neural Networks and Deep Learning》（美）Michael Nielsen 著英文版.pdf

Neural Networks and Deep Learning - 神经网络与深度学习中英双版本