the circularly symmetric neighborhood g
t;p
ðt ¼ t
c
L; t
c
;
t
c
þ L; p ¼ 0; ;P 1Þ, giving
V ¼ vðg
t
c
L;c
g
t
c
;c
;g
t
c
L;0
g
t
c
;c
; ;
g
t
c
L;P 1
g
t
c
;c
;g
t
c
;c
;g
t
c
;0
g
t
c
;c
; ;
g
t
c
;P 1
g
t
c
;c
;g
t
c
þL;0
g
t
c
;c
; ;
g
t
c
þL;P 1
g
t
c
;c
;g
t
c
þL;c
g
t
c
;c
Þ:
ð2Þ
Then, we assume that differences g
t;p
g
t
c
;c
are indepen-
dent of g
t
c
;c
, which allow us to factorize (2):
V vðg
t
c
;c
Þvðg
t
c
L;c
g
t
c
;c
;g
t
c
L;0
g
t
c
;c
; ;
g
t
c
L;P1
g
t
c
;c
;g
t
c
;0
g
t
c
;c
; ;g
t
c
;P1
g
t
c
;c
;
g
t
c
þL;0
g
t
c
;c
; ;g
t
c
þL;P1
g
t
c
;c
;g
t
c
þL;c
g
t
c
;c
Þ:
In practice, exact independence is not warranted; hence,
the factorized distribution is only an approximation of the
joint distribution. However, we are willing to accept a
possible small loss of information as it allows us to achieve
invariance with respect to shifts in gray scale. Thus, similar to
LBP in ordinary texture analysis [6], the distribution vðg
t
c
;c
Þ
describes the overall luminance of the image, which is
unrelated to the local image texture and, consequently, does
not provide useful information for DT analysis. Hence, much
of the information in the original joint gray-level distribution
(1) is conveyed by the joint difference distribution:
V
1
¼ v ðg
t
c
L;c
g
t
c
;c
;g
t
c
L;0
g
t
c
;c
; ;
g
t
c
L;P1
g
t
c
;c
;g
t
c
;0
g
t
c
;c
; ;g
t
c
;P1
g
t
c
;c
;
g
t
c
þL;0
g
t
c
;c
; ;g
t
c
þL;P1
g
t
c
;c
;g
t
c
þL;c
g
t
c
;c
Þ:
This is a highly discriminative texture operator. It
records the occurrences of various patterns in the neighbor-
hood of each pixel in a ð2ðP þ 1ÞþP ¼ 3P þ 2Þ-dimen-
sional histogram.
We achieve invariance with respect to the scaling of the
gray scale by considering simply the signs of the differences
instead of their exact values:
V
2
¼ v
sðg
t
c
L;c
g
t
c
;c
Þ;sðg
t
c
L;0
g
t
c
;c
Þ; ;
sðg
t
c
L;P1
g
t
c
;c
Þ;sðg
t
c
;0
g
t
c
;c
Þ; ;
sðg
t
c
;P1
g
t
c
;c
Þ;sðg
t
c
þL;0
g
t
c
;c
Þ; ;
sðg
t
c
þL;P1
g
t
c
;c
Þ;sðg
t
c
þL;c
g
t
c
;c
Þ
;
ð3Þ
where sðxÞ¼
1;x 0
0;x< 0
.
To simplify the expression of V
2
, we use V
2
¼ vðv
0
; ;
v
q
; ;v
3Pþ1
Þ, and q corresponds to the index of values in
V
2
orderly. By assigning a binomial factor 2
q
for each
sign sðg
t;p
g
t
c
;c
Þ, we transform (3) into a unique V LBP
L;P;R
number that characterizes the spatial structure of the local
volume DT:
V LBP
L;P;R
¼
X
3Pþ1
q¼0
v
q
2
q
: ð4Þ
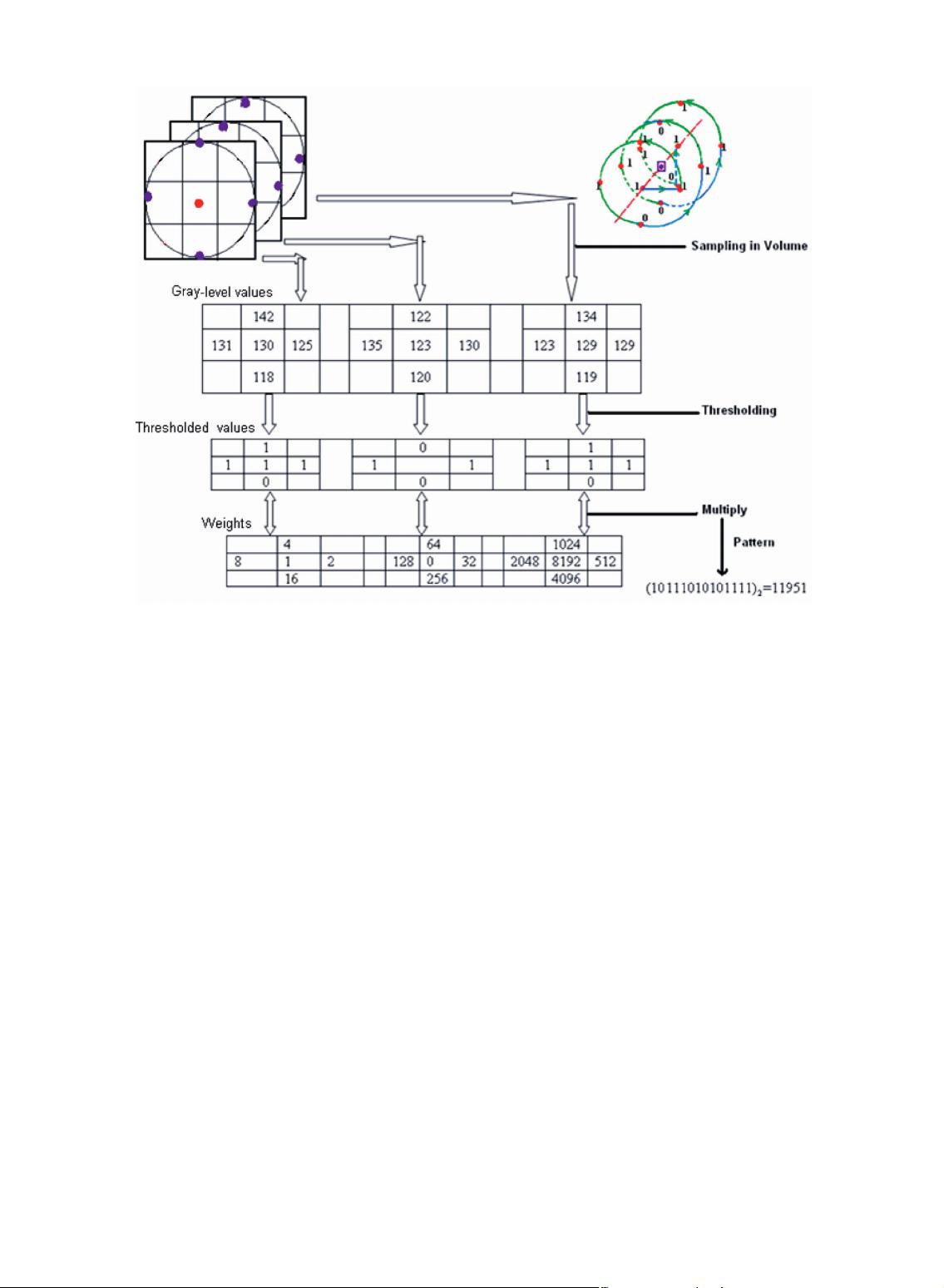
Fig. 1 shows the whole computing procedure for
V LBP
1;4;1
. We begin by sampling neighboring points in
the volume and then thresholding every point in the
neighborhood with the value of the center pixel to get a
binary valu e. Finally, we produce the VLBP code by
ZHAO AND PIETIKA
¨
INEN: DYNAMIC TEXTURE RECOGNITION USING LOCAL BINARY PATTERNS WITH AN APPLICATION TO FACIAL... 917
Fig. 1. Procedure of V LBP
1;4;1
.






















