一阶与二阶RC电路响应探究

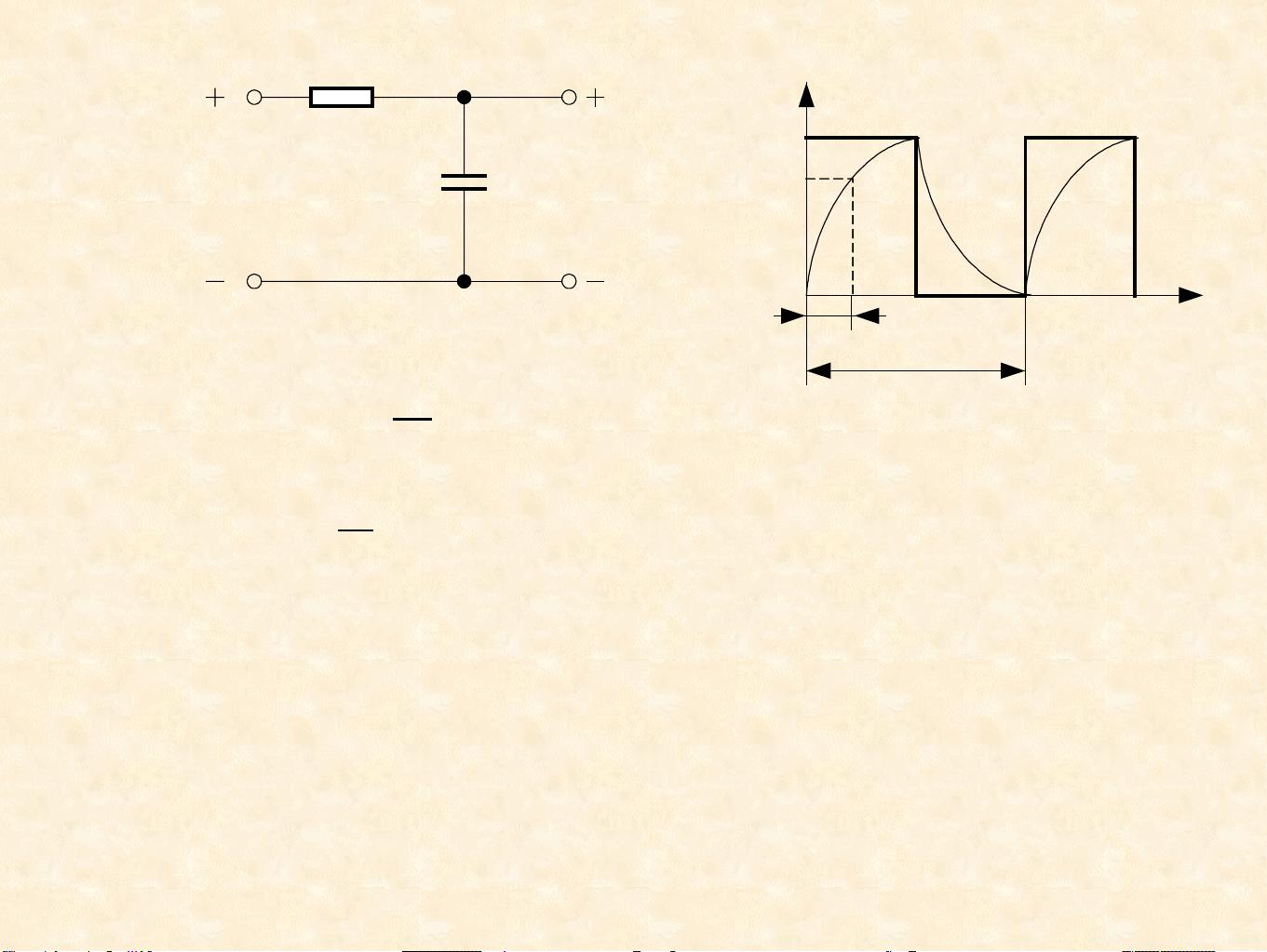
"RC电路是电子工程中常见的一种电路，由电阻(R)和电容(C)组成，广泛应用于信号处理和滤波等领域。本实验主要关注一阶和二阶RC电路的响应特性，以及时间常数对电路行为的影响。通过实验，可以了解微分电路和积分电路的工作原理，并分析二阶电路的三种状态轨迹。" 一阶RC电路是含有一个电阻和一个电容的简单电路，其时间常数τ定义为R*C。在零输入响应(ZIR)中，电容C通过电阻R放电，电压会按照指数规律衰减，最终趋近于零。零状态响应(ZSR)则是当电路接通电源后，电容C通过电阻R充电的过程。全响应是ZIR和ZSR的组合，它描述了电容电压从初始状态到最终稳定状态的变化过程。 实验中，通过测量不同时间常数τ的一阶RC电路，可以观察到曲线衰减速度的不同。τ越大，电容电压衰减得越慢。例如，τ=1时，电压衰减至0.368U0需要一个时间常数，而τ=2时，需要两个时间常数才衰减到同样水平。 微分电路是一种特殊的一阶RC电路，它在τ<<T/2的条件下，能够近似输出输入电压的微分。当输入信号频率较低，满足τ<<1/(10f)时，微分电路会产生尖脉冲输出，这些脉冲的幅度是输入方波幅度的两倍。时间常数τ越小，脉冲越尖锐。 积分电路则在τ>>T/2且uC<<uR的条件下，电容电压近似等于输入电压的积分。这种电路常用于平滑信号或实现电压到时间的转换。积分电路的输出波形相对平缓，与输入信号形状相反，用于抵消尖峰或消除高频噪声。 二阶RC电路增加了第二个电容，使得响应更复杂，包括过阻尼、欠阻尼和临界阻尼三种状态轨迹。通过实验，可以研究电容值和电阻值如何影响这些响应，以及它们对系统稳定性和上升时间的影响。 总结来说，RC电路在电路设计中扮演着重要角色，不仅涉及到基本的充放电特性，还用于实现信号的微分和积分，以及复杂的动态响应分析。通过实验和理论学习，工程师能更好地理解和应用RC电路在实际系统中的功能。