SPSS线性回归分析详解
107 浏览量
更新于2024-07-16
2
收藏 250KB PPT 举报
"本资料是关于SPSS进行线性回归分析的PPT,主要介绍了线性回归的概念、原理以及在SPSS中的应用方法。"
线性回归是一种统计分析方法,用于研究两个或多个定量变量之间的关系,特别是当一个变量(自变量)对另一个变量(因变量)产生影响时。在描述性统计中,数据处理的目标是从大量数据中提取有价值的信息,而线性回归则提供了一种工具,用于建立变量间的因果关系模型,并具备预测能力。
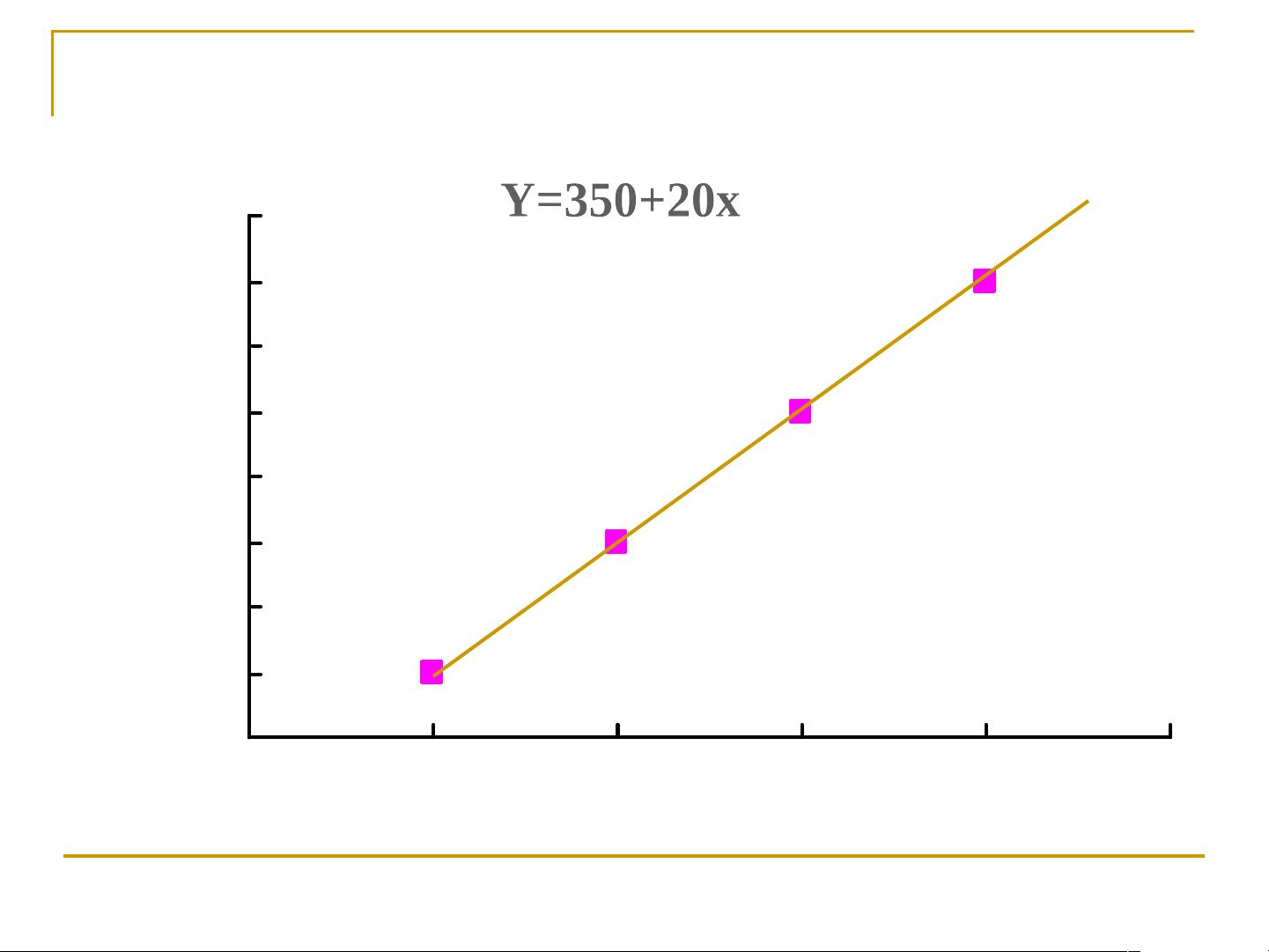
线性回归的统计原理基于一元线性方程,通常形式为 \( y = a + bx \),其中 \( y \) 是因变量,\( x \) 是自变量,\( a \) 是截距,代表当 \( x \) 为零时 \( y \) 的期望值,而 \( b \) 是斜率,表示 \( x \) 每变化一个单位,\( y \) 预期的变化量。在实际应用中,这些参数是通过对大量观测数据进行拟合来估计的,采用的方法是“最小二乘法”,即找到一条直线,使得所有数据点到这条直线的垂直距离平方和最小。
在线性回归中,有几个重要的假设条件需要满足:
1. 线性趋势:自变量与因变量之间必须存在线性关系。
2. 独立性:因变量的每个观测值之间相互独立,不受其他观测值的影响。
3. 正态性:自变量的任何线性组合,其误差项(残差)应服从正态分布。
4. 方差齐性:自变量的线性组合的误差项应具有相同的方差。
在SPSS软件中,进行线性回归分析可以通过“Linear Regression”对话框进行设置。用户可以选择“Enter”方法,将所有自变量一次性引入模型,或者选择“Stepwise”逐步法,依据预设的标准筛选变量进入模型。逐步法会根据变量对因变量的贡献大小,按顺序加入或移除变量,以优化模型性能。
线性回归分析的结果通常包括回归系数、截距、R平方、调整R平方、F统计量和显著性等统计量,这些可以帮助评估模型的拟合优度和变量的重要性。此外,残差分析也是评估模型是否符合假设的重要手段,例如,检查残差的正态性分布和方差一致性。
通过线性回归分析,可以预测因变量的值,例如在教育和薪资的例子中,可以预测随着教育年限的增加,薪资水平的相应变化。这对于政策制定、市场预测和科学研究等领域都具有重要的应用价值。然而,需要注意的是,线性回归模型建立的因果关系只是统计意义上的关联,并不能证明因果关系的真实性,还需要结合理论背景和实证研究来确认。
2019-12-04 上传
2021-10-07 上传
2021-09-16 上传
2021-09-16 上传
2021-12-09 上传
2022-11-15 上传
weixin_43360470
- 粉丝: 0
- 资源: 3
最新资源
- 深入了解Django框架:Python中的网站开发利器
- Spring Boot集成框架示例:深入理解与实践
- 52pojie.cn捷速OCR文字识别工具实用评测
- Unity实现动态水体涟漪效果教程
- Vue.js项目实践:饭否每日精选日历Web版开发记
- Bootbox:用Bootstrap实现JavaScript对话框新体验
- AlarStudios:Swift开发教程及资源分享
- 《火影忍者》主题新标签页壁纸:每日更新与自定义天气
- 海康视频H5player简易演示教程
- -roll20脚本开发指南:探索roll20-master包-
- Xfce ClassicLooks复古主题更新,统一Linux/FreeBSD外观
- 自建物理引擎学习刚体动力学模拟
- Python小波变换工具包pywt的使用与实例
- 批发网导航程序:自定义模板与分类标签
- 创建交互式钢琴键效果的JavaScript库
- AndroidSunat应用开发技术栈及推介会议