傅里叶变换与信号分析：从正交分解到滤波

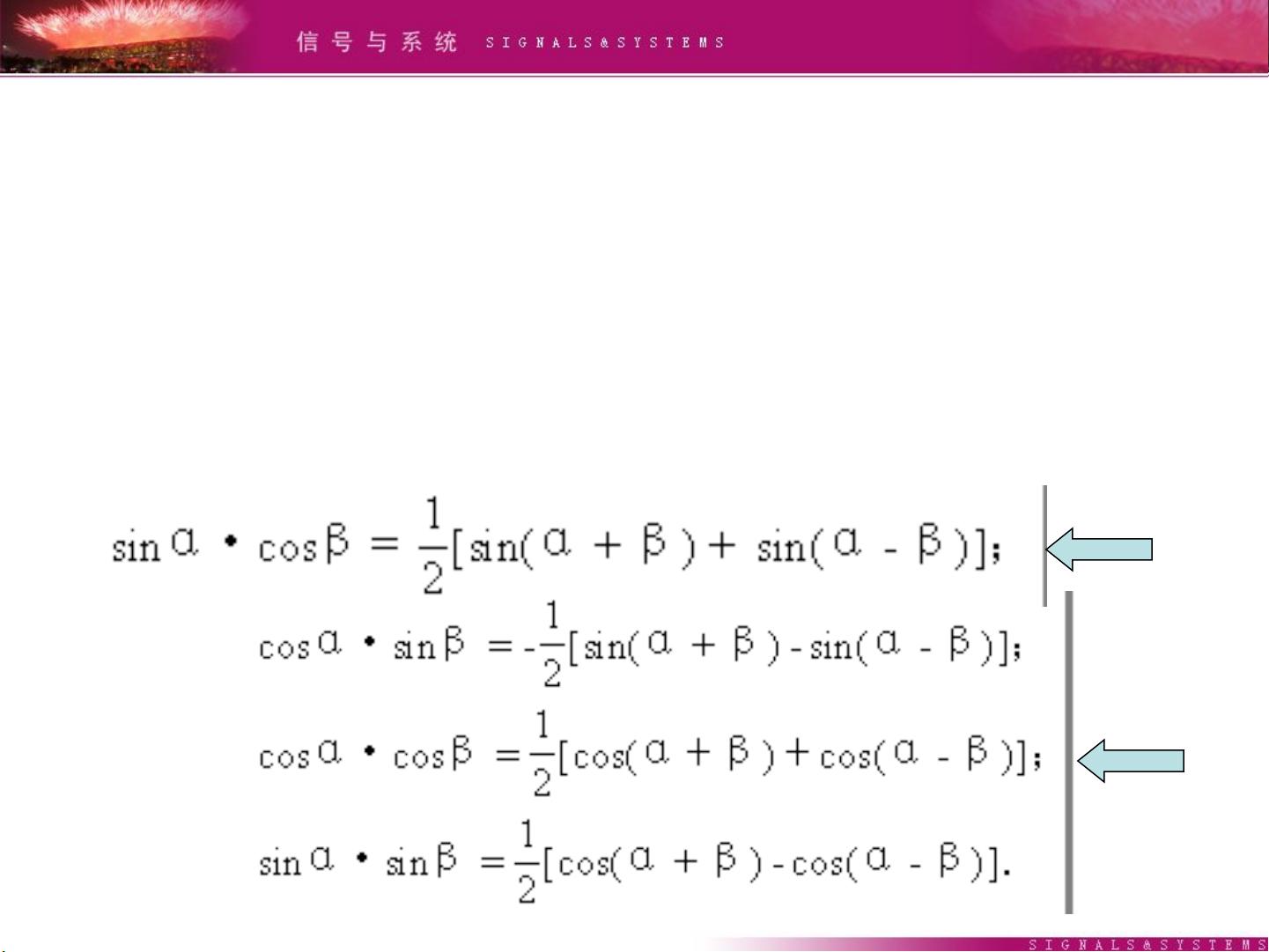
"本讲义主要讲解信号与系统的第三章——傅里叶变换，包括信号的正交分解、傅里叶级数、周期信号的频谱、傅里叶变换、抽样信号与抽样定理、系统的频域分析以及信号的传输与滤波等内容。特别强调了傅里叶级数在各个领域的应用，如物理学、信号处理等。讲义中还涉及到傅立叶的历史贡献，以及正交矢量和正交函数的概念。" 正文: 在深入探讨傅里叶变换之前，我们需要先理解正交分解的基础。正交矢量是指在一定空间中相互垂直的向量，它们之间的内积（点积）为零。在二维或三维空间中，正交矢量可以用来表示任何向量，而在更高维度的空间，正交矢量集用于表示复杂系统中的多个独立变量。 正交函数的概念是傅里叶变换的基础。如果两个函数在特定区间上的积分乘积为零，那么这两个函数就是在这个区间上的正交函数。例如，正弦函数和余弦函数在任意周期内就是正交的。在信号处理领域，正交函数集被用来分解信号，使得复杂的信号可以表示为简单的正交函数的线性组合。 傅里叶级数是将周期性信号分解为一系列不同频率的正弦和余弦函数的级数。这个理论最早由傅立叶提出，他在研究热传导问题时发现了这一方法。傅里叶级数的应用广泛，例如在气候研究中，通过正弦函数可以分析地球的周期性气候变化；在电力系统中，正弦波形描述了交流电的电压和电流。 傅里叶变换进一步扩展了这一思想，适用于非周期信号。它将时间域的信号转化为频域的表示，揭示了信号的频率成分。这对于分析信号的性质，如滤波、通信和图像处理等具有重要意义。 抽样信号与抽样定理是傅里叶变换的一个关键应用，它阐述了如何从连续时间信号中抽取离散样本，而不会丢失原始信号的信息。抽样定理规定了为了无失真地恢复信号，所需的最小抽样频率。 系统的频域分析利用傅里叶变换将系统在时间域的响应转化为频率域，这有助于理解和设计滤波器，以消除或增强信号的某些频率成分。信号的传输与滤波是通信系统中的重要环节，通过频域分析可以优化信号的传输效率和质量。 总结来说，本讲义不仅涵盖了傅里叶变换的基本理论，还深入探讨了其在实际应用中的各种方面，特别是正交分解和正交函数集的概念，这些都是理解和应用傅里叶变换的关键。通过学习这些内容，读者能够更好地理解和处理各种信号与系统问题。