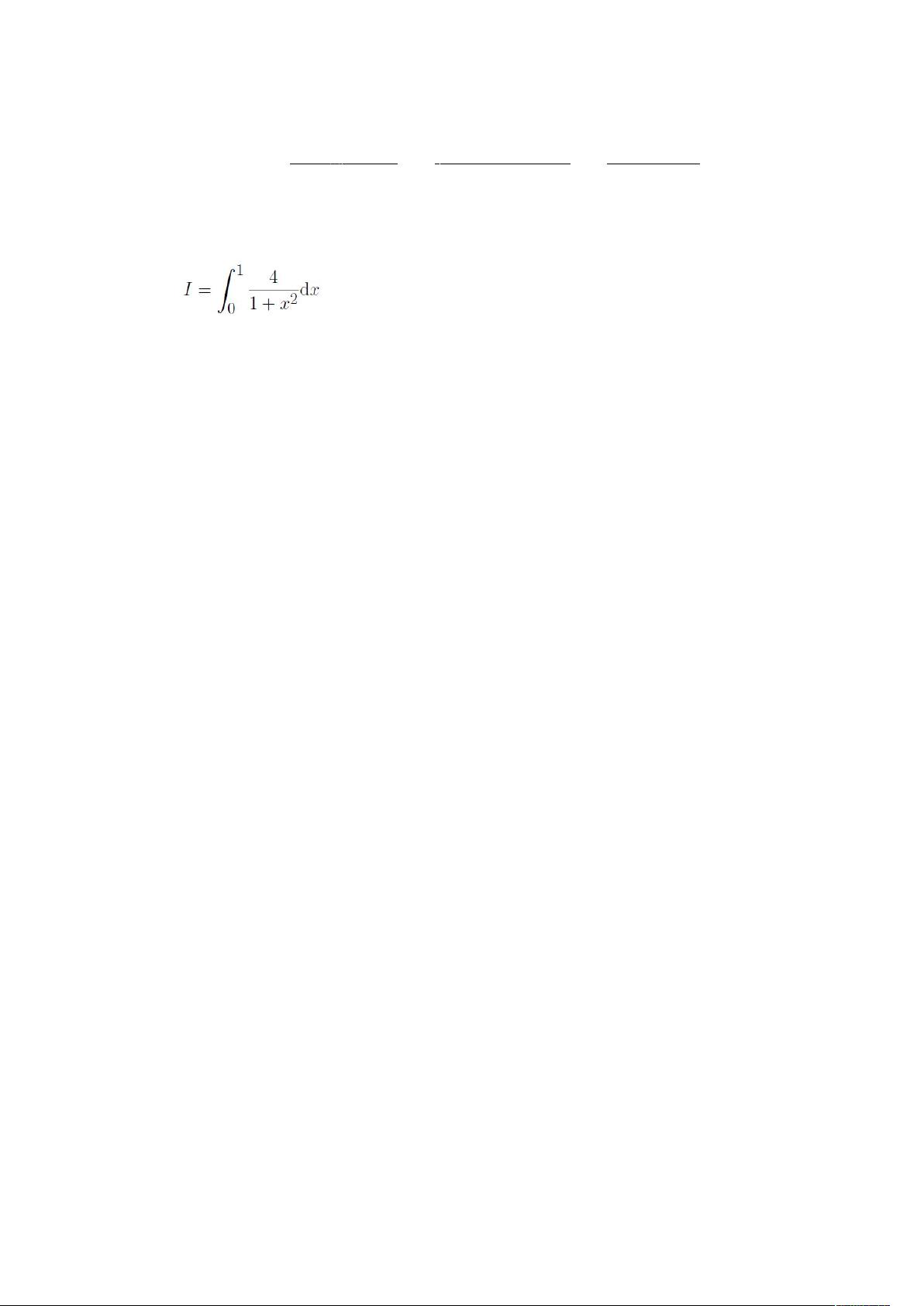龙贝格求积算法在实验2中的高精度实现与C语言代码

本资源是一份关于龙贝格求积算法实现的实验报告，由詹文淇同学在2019年计科2班完成。实验任务是利用复化梯形公式进行高精度求积，具体案例参考教材P110的例4.2。龙贝格求积算法是一种数值积分方法，它通过递归地将积分区间细化，通过外推多项式来逼近原函数的积分值，从而达到提高精度的目的。 该算法的核心是二维数组T，其中T[i][j]表示使用2i个子区间进行j次外推的积分值。T[i][0]特别重要，作为0次外推，采用自适应复化梯形法计算，后续的迭代公式为T[i][j] = (4j * T[i][j-1] - T[i-1][j-1]) / (4j - 1)，这是一种递归公式，每次迭代都会更新当前精度级别的积分近似。 终止条件设定为当外推次数达到一定阈值（例如14次），且相邻两次迭代的误差|T[i][i-1] - T[i-1][i-1]|小于预设的容差ε（在这个例子中，ε=1e-5），则停止迭代。此时，最后一次外推的数据T[i][i]即为积分的最终结果。 程序流程中，首先初始化积分区间h为b-a，步长n为1，然后用递归的方式计算T[i][j]，同时记录误差并调整子区间数。使用C语言（DEVC++）编写，涉及了基本的数学库函数，如求平方根、函数值计算以及整数次幂运算。关键部分包括计算函数getRombergFunction，用于获取自变量x对应函数值，以及自定义的pow函数实现整数次幂。 这份文档提供了龙贝格求积算法的具体实现步骤和代码，对于理解数值积分的高级技巧和编程实现具有很高的参考价值。通过学习和实践这个算法，学生可以掌握如何利用计算机进行高精度积分计算，并能根据实际需求调整算法以优化精度和效率。