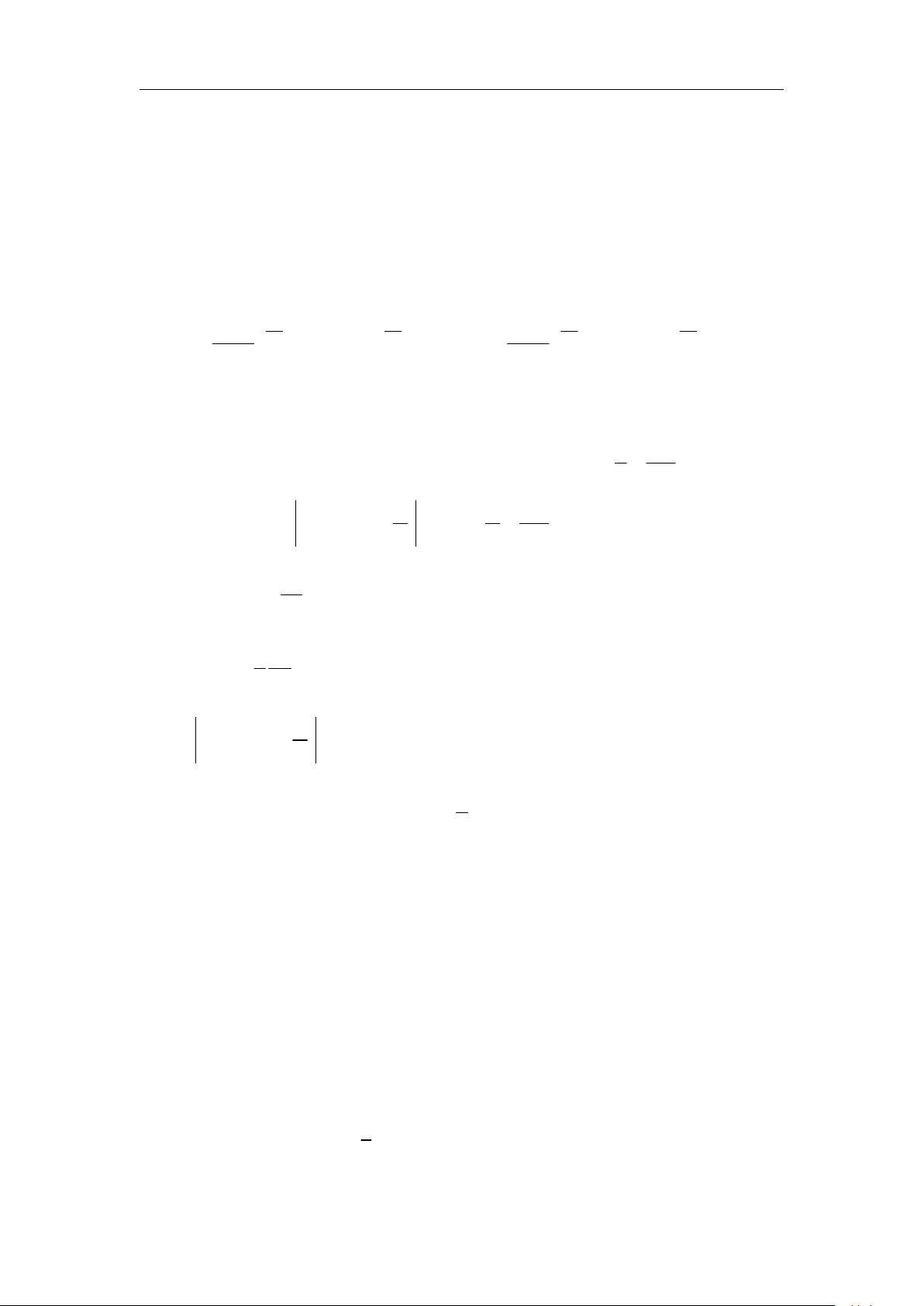1992考研数学一真题详解:填空与选择题解析
需积分: 0 126 浏览量
更新于2024-08-05
收藏 408KB PDF 举报
1992年考研数学一真题解析主要集中在填空题和选择题部分。首先,一道题目涉及的是隐函数求导的应用。函数
()
y
yx
通过隐函数的形式给出,要求解关于x的导数。利用复合函数求导法则,先对方程两边关于x求导,将y视为x的函数,得出
y
xy
y
dx
e
x
xy
,进而得到y关于x的导数。
第二题考察多元函数的梯度和向量运算。给定函数u的偏导数,计算梯度gradu,并将其与矩阵M相乘,结果为
2
2
2
1
2,4,4
1,2,2
1
2
(2)
9
M
gradu
。这涉及到了多元函数的偏导数和梯度向量的概念,以及它们在向量代数中的应用。
第三题是一道关于区间积分的问题,要求计算定积分
2
1
x
π
dx
。此题考查基本的积分计算,涉及到区间积分的求解和特定函数的积分性质。
整体来看,这些题目涵盖了微积分的基本概念和方法,包括隐函数求导、多元函数的偏导数和梯度、以及基本积分技巧,这些都是数学一考试中常考的基础知识点。解答这类题目时,考生需要熟练掌握函数求导的规则,特别是复合函数和多元函数的求导,同时具备一定的积分理论基础。
166 浏览量
266 浏览量
2022-08-03 上传
2021-11-06 上传
2021-11-06 上传
2021-11-06 上传
战神哥
- 粉丝: 1008
- 资源: 325
最新资源
- Tarea-1
- Class-Work:证明熟练掌握sql,pandas,numpy和scikit学习
- CANVAS-JS:+ JS-Reto Platzi
- reaktor_warehouse:Reaktor对2021年夏季的预分配
- 室外建筑模型设计效果图
- HighChartsProject
- 学生基本信息表excel模版下载
- MOO Maker:经典“MOO”或“Cows n Bulls”游戏的变种。-matlab开发
- overlay-simple
- bot-lock
- ch3casestudy-jnwyatt:ch3casestudy-jnwyatt由GitHub Classroom创建
- shoppingcar:测试
- gitlab-sync:一次同步GitLab存储库组的实用程序
- 解决java.security.InvalidKeyException: Illegal key size
- 艺术展厅3D模型素材
- thick_line(x,y,thickness):生成与输入线对应的粗线的边缘坐标-matlab开发