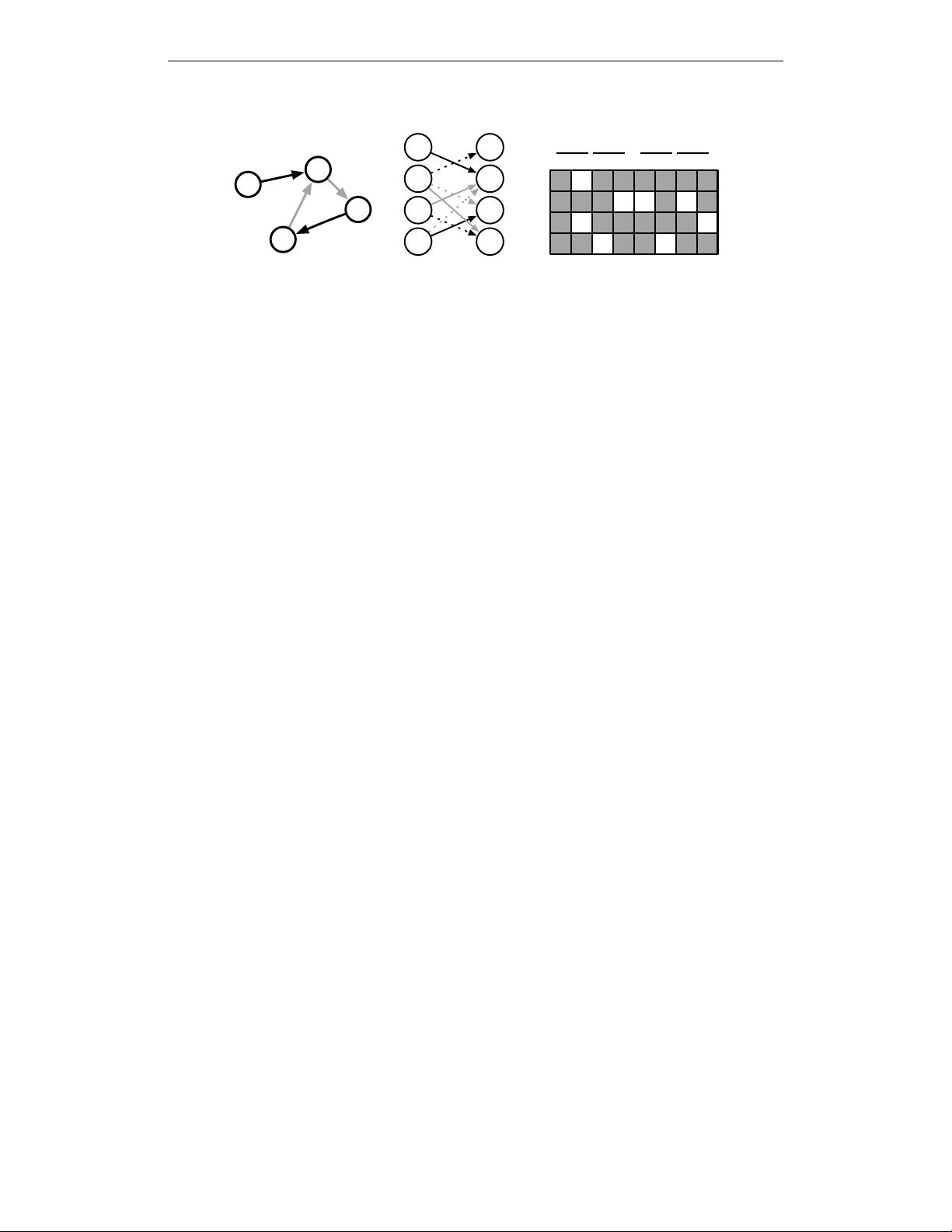
Published as a conference paper at ICLR 2016
3
4
1
2
h
(t1)
2
h
(t1)
1
h
(t1)
3
h
(t1)
4
h
(t)
4
h
(t)
3
h
(t)
2
h
(t)
1
B
C
C
B
1
2
3
4
1 2 3 4
Outgoing Edges
B’ C’
C’
B’
1 2 3 4
Incoming Edges
| {z }
| {z }
(a) (b) (c) A =
A
(out)
, A
(in)
Figure 1: (a) Example graph. Color denotes edge types. (b) Unrolled one timestep. (c) Parameter
tying and sparsity in recurrent matrix. Letters denote edge types with
B
0
corresponding to the reverse
edge of type B. B and B
0
denote distinct parameters.
The matrix
A ∈ R
D|V|×2D|V|
determines how nodes in the graph communicate with each other. The
sparsity structure and parameter tying in
A
is illustrated in Fig. 1. The sparsity structure corresponds
to the edges of the graph, and the parameters in each submatrix are determined by the edge type
and direction.
A
v:
∈ R
D×2D|V|
is the submatrix of
A
containing the rows corresponding to node
v
. Eq. 1 is the initialization step, which copies node annotations into the first components of the
hidden state and pads the rest with zeros. Eq. 2 is the step that passes information between different
nodes of the graph via incoming and outgoing edges with parameters dependent on the edge type
and direction.
a
(t)
v
∈ R
2D
contains activations from edges in both directions. The remaining are
GRU-like updates that incorporate information from the other nodes and from the previous timestep
to update each node’s hidden state.
z
and
r
are the update and reset gates,
σ(x) = 1/(1 + e
−x
)
is the
logistic sigmoid function, and
is element-wise multiplication. We initially experimented with a
vanilla recurrent neural network-style update, but in preliminary experiments we found this GRU-like
propagation step to be more effective.
3.3 OUTPUT MODELS
There are several types of one-step outputs that we would like to produce in different situations. First,
GG-NNs support node selection tasks by making
o
v
= g(h
(T )
v
, x
v
)
for each node
v ∈ V
output node
scores and applying a softmax over node scores. Second, for graph-level outputs, we define a graph
level representation vector as
h
G
= tanh
X
v∈V
σ
i(h
(T )
v
, x
v
)
tanh
j(h
(T )
v
, x
v
)
!
, (7)
where
σ(i(h
(T )
v
, x
v
))
acts as a soft attention mechanism that decides which nodes are relevant to the
current graph-level task.
i
and
j
are neural networks that take the concatenation of
h
(T )
v
and
x
v
as
input and outputs real-valued vectors. The tanh functions can also be replaced with the identity.
4 GATED GRAPH SEQUENCE NEURAL NETWORKS
Here we describe Gated Graph Sequence Neural Networks (GGS-NNs), in which several GG-NNs
operate in sequence to produce an output sequence o
(1)
. . . o
(K)
.
For the
k
th
output step, we denote the matrix of node annotations as
X
(k)
= [x
(k)
1
; . . . ; x
(k)
|V|
]
>
∈
R
|V|×L
V
. We use two GG-NNs
F
(k)
o
and
F
(k)
X
:
F
(k)
o
for predicting
o
(k)
from
X
(k)
, and
F
(k)
X
for
predicting
X
(k+1)
from
X
(k)
.
X
(k+1)
can be seen as the states carried over from step
k
to
k + 1
.
Both
F
(k)
o
and
F
(k)
X
contain a propagation model and an output model. In the propagation models,
we denote the matrix of node vectors at the
t
th
propagation step of the
k
th
output step as
H
(k,t)
=
[h
(k,t)
1
; . . . ; h
(k,t)
|V|
]
>
∈ R
|V|×D
. As before, in step
k
, we set
H
(k,1)
by
0
-extending
X
(k)
per node. An
overview of the model is shown in Fig. 2. Alternatively,
F
(k)
o
and
F
(k)
X
can share a single propagation
model, and just have separate output models. This simpler variant is faster to train and evaluate, and
4
剩余19页未读，继续阅读
sidfj
- 粉丝: 0
- 资源: 5
我的内容管理
展开
最新资源
- Lombok 快速入门与注解详解
- SpringSecurity实战：声明式安全控制框架解析
- XML基础教程：从数据传输到存储解析
- Matlab实现图像空间平移与镜像变换示例
- Python流程控制与运算符详解
- Python基础：类型转换与循环语句
- 辰科CD-6024-4控制器说明书：LED亮度调节与触发功能解析
- AE particular插件全面解析：英汉对照与关键参数
- Shell脚本实践：创建tar包、字符串累加与简易运算器
- TMS320F28335：浮点处理器与ADC详解
- 互联网基础与结构解析：从ARPANET到多层次ISP
- Redhat系统中构建与Windows共享的Samba服务器实战
- microPython编程指南：从入门到实践
- 数据结构实验：顺序构建并遍历链表
- NVIDIA TX2系统安装与恢复指南
- C语言实现贪吃蛇游戏基础代码
资源上传下载、课程学习等过程中有任何疑问或建议，欢迎提出宝贵意见哦~我们会及时处理！
点击此处反馈
