Python编程:蒙特卡洛法计算定积分实战解析
159 浏览量
更新于2024-08-31
3
收藏 192KB PDF 举报
"Python编程通过蒙特卡洛法计算定积分详解"
在数学中,定积分是微积分的基本概念之一,用于计算曲线下的面积、物理问题中的位移、速度和加速度等。然而,对于某些复杂的函数,直接计算定积分可能非常困难。这时,我们可以借助计算机和编程方法来求解,其中,蒙特卡洛法是一种简单且实用的方法。
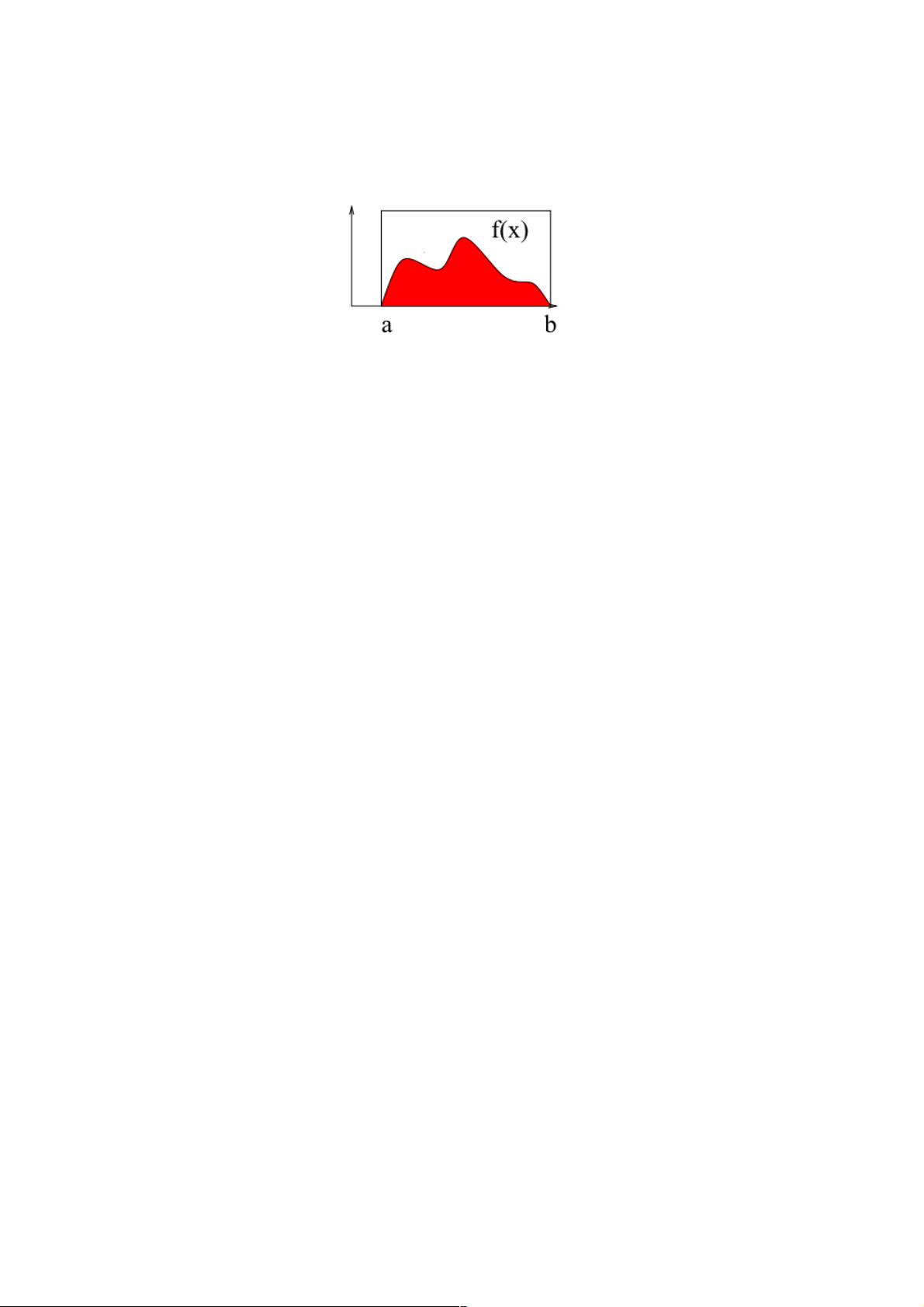
蒙特卡洛法是一种统计模拟方法,它利用随机抽样或统计试验来解决问题。在计算定积分时,基本思想是将积分区间划分为多个小区域,然后随机生成大量点,统计这些点落在被积函数上方的比例。这个比例乘以区间长度,就能近似得到积分的值。
在Python中,我们可以利用numpy库进行随机数生成,matplotlib库进行绘图,实现蒙特卡洛法计算定积分。以下是一个具体的实现示例:
```python
import numpy as np
import matplotlib.pyplot as plt
# 定义被积函数
def f(x):
return x**2 + 4 * x * np.sin(x)
# 定义被积函数的精确积分
def intf(x):
return x**3 / 3.0 + 4.0 * np.sin(x) - 4.0 * x * np.cos(x)
# 设置积分区间
a = 2
b = 3
# 随机生成N个点
N = 10000
X = np.random.uniform(low=a, high=b, size=N)
Y = f(X)
# 计算蒙特卡洛法的积分近似值
Imc = (b - a) * np.sum(Y) / N
# 计算精确积分值
exact_val = intf(b) - intf(a)
print("蒙特卡洛估计值 =", Imc, "精确数值 =", exact_val)
```
这段代码首先定义了被积函数`f(x)`和其精确积分`intf(x)`,接着在区间[2, 3]上生成N个均匀分布的随机点,计算这些点对应的函数值,并通过平均高度乘以区间长度得到积分的近似值。最后,输出蒙特卡洛法的估计值和精确值进行比较。
为了研究蒙特卡洛法的准确性与采样点数的关系,可以进一步改变N的值,重复上述过程。这将生成一系列估计值,从而观察随着样本数量增加,积分近似值如何逼近精确值。
蒙特卡洛法的优点在于简单易行,尤其适用于高维积分问题。但它的缺点也很明显,即精度依赖于随机样本的数量,需要大量的计算资源。不过,由于现代计算机性能强大,即使对于大规模问题,也能在合理的时间内完成计算。
Python结合蒙特卡洛法提供了一种有效的方法来处理复杂的定积分问题,使得我们能够利用编程工具解决数学中的难题。在实际应用中,可以通过调整样本数量找到一个平衡点,既能满足精度要求,又不会过于消耗计算资源。
weixin_38569569
- 粉丝: 7
- 资源: 931