IBM SPSS：多元方差分析实战教程 - 比较多时期儿童发育数据

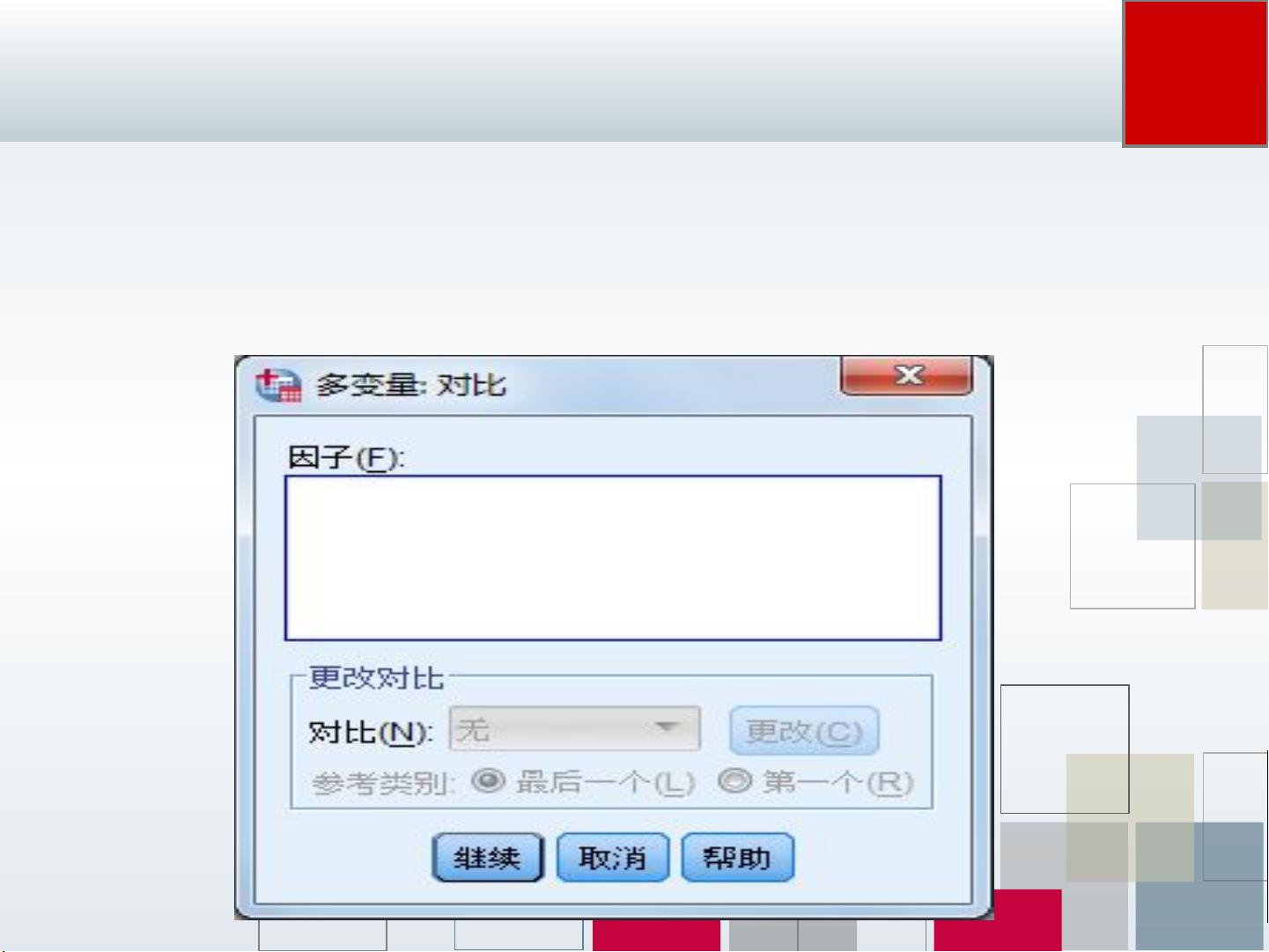
第22章的"多元方差分析"是统计分析中的一个重要概念，主要应用于处理涉及多个应变量的实验设计，它在IBM-SPSS软件中得到了应用。与一元方差分析相比，多元方差分析（Multivariate Analysis of Variance, MANOVA）处理的是多个响应变量之间的差异，这些变量通常需要满足独立性、正态分布和方差齐性等基本假设。 在单因素设计的多元方差分析中，例如例22.1，研究者关注的是某地不同时期20名8岁男童的身高、体重和胸围等三个指标是否与10年前的平均值存在显著差异。首先，数据预处理是关键步骤，通过计算变量对话框将原始数据转换为新的变量，如身高减去平均值得到偏差。接着，在SPSS中选择"分析"菜单下的"一般线性模型" -> "多变量"，设置因变量（反应变量）、固定因子、协变量以及可能的权重，如WLS（权重最小二乘法）。 在模型对话框中，用户可以选择不同的对比方法，并在选项对话框中调整参数以获取精确的结果。多元方差分析的结果通常包括样本观察值与总体均数的差异、统计检验的F值，以及这些F值是否达到统计学上的显著性水平。在例22.1中，结果显示四种统计量的F值都具有统计学意义，这表明当前调查的儿童生长发育情况确实与十年前的平均值有显著差异。 多因素资料的多元方差分析则更为复杂，它涉及到两个或更多因素的影响，每个因素可能有不同的水平或类别。这种分析能同时考察多个自变量对多个应变量的影响，有助于深入理解变量间的交互作用。进行这类分析时，需要确保所有相关的交互效应和主效应都被适当地纳入模型。 总结来说，第22章的内容涵盖了多元方差分析的基础理论、实际操作步骤和结果解读，它是统计分析工具箱中的重要组成部分，对于理解和解释多变量数据集中的模式和差异具有重要意义。