Logistic回归模型与分类

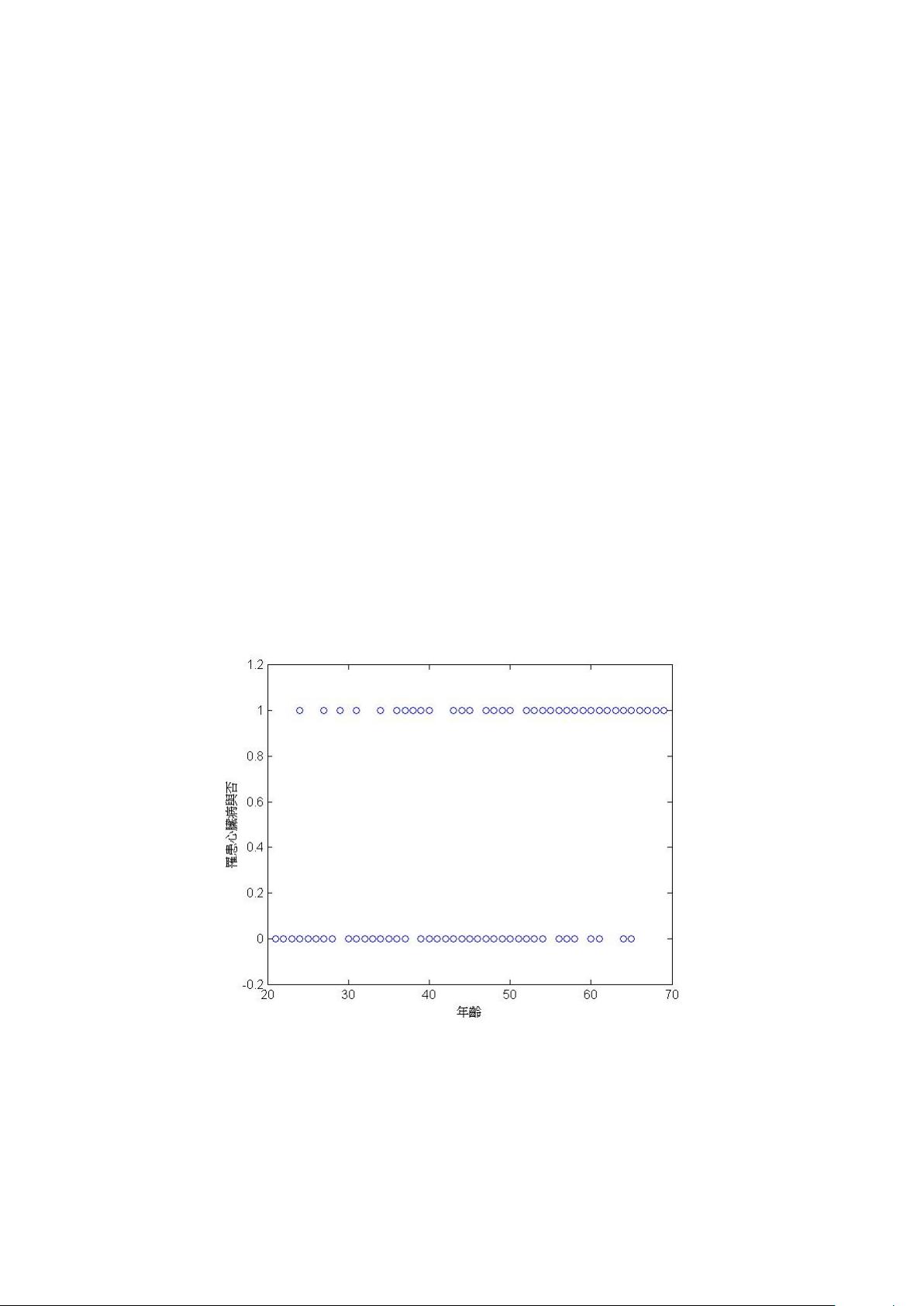
"M_logistic分界线由来——Logistic回归模型及其应用" Logistic回归是一种统计分析方法，主要用于处理因变量为分类数据的情况，特别是二分类问题。它的起源在于解决当因变量的概率分布呈现S型曲线（sigmoid函数）时，如何通过线性模型来描述自变量与因变量之间的关系。这种曲线形状使得Logistic回归能够预测一个事件发生的概率，而不是连续的数值。 1.1 Logistic回归介绍 Logistic回归模型的核心在于它能够将线性组合（β0 + β1x1 + β2x2 + ... + βkxk）转换为介于0和1之间的概率值。这个转换过程通过sigmoid函数完成，即： Pr(G=1|X=x) = 1 / (1 + e^(-f(x))) 其中，f(x) = β0 + β1x1 + β2x2 + ... + βkxk 是线性部分，β0、β1、...、βk是待估计的参数。Sigmoid函数的特性使得输出始终在0到1之间，这正好对应了概率的取值范围。 1.2 Logit变换与最大似然估计 Logistic回归中的分界线，或者说决策边界，是由logit变换定义的： z = log[Pr(G=1|X=x) / Pr(G=2|X=x)] = β0 + β1x 这里的z是log odds，即两个类别的对数优势比。通过最大化似然函数，我们可以估计出参数β0、β1、...、βk的值。这种方法称为最大似然估计，它在许多统计模型中都是一种常用的参数估计方法。 1.3 LDA与Logistic回归的对比 线性判别分析（LDA）在处理分类问题时，假设因变量服从正态分布，并且不同类别间的协方差矩阵相同。LDA的决策边界是基于后验概率的logit转换等于0。然而，Logistic回归不依赖于这些假设，它可以处理非正态分布的数据，因此具有更广泛的应用场景。 1.4 应用场景 Logistic回归在很多领域都有应用，比如医学研究中的疾病预测、市场分析中的购买行为预测、社会科学中的态度调查分析等。它能够捕捉自变量与因变量之间的非线性关系，同时提供概率预测，这对于理解变量间的影响和做出决策非常有用。 M_logistic分界线是Logistic回归模型中的一个重要概念，它通过非线性的logit变换，为分类问题提供了有效的解决方案。通过对参数的最大似然估计，Logistic回归能够适应各种复杂的数据分布，成为处理分类问题的一种强大工具。