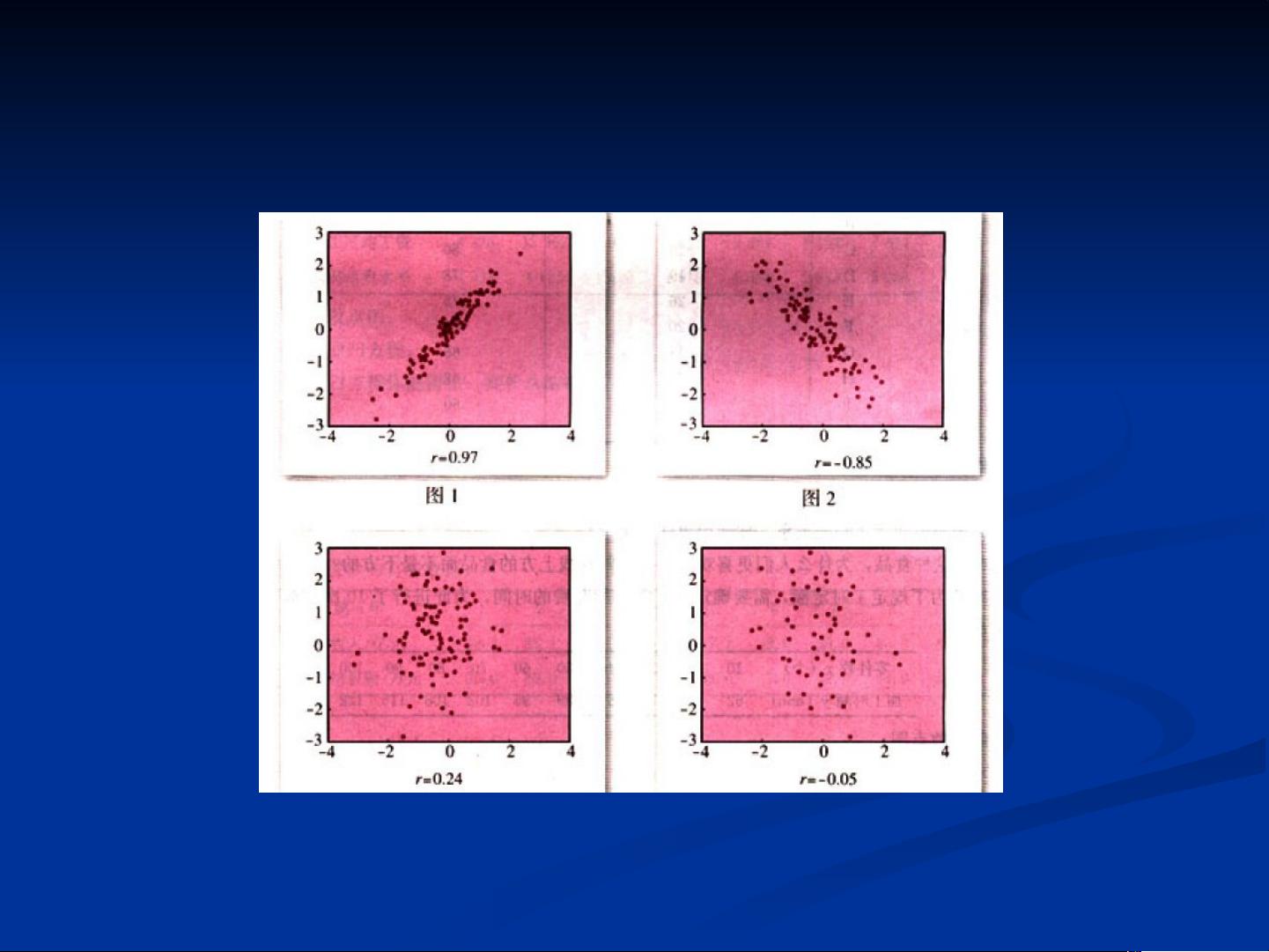
相关关系与回归分析初步应用：从基本思想到实际场景的解析

回归分析是一种统计分析方法，用于研究两个或多个变量之间的关系。它的基本思想是通过建立一个数学模型来描述自变量与因变量之间的关系，并利用这个模型来预测或解释因变量的变化。回归分析广泛应用于各种领域，如经济学、商业、社会科学、医学和工程等。 回归分析的基本思想及其初步应用是通过建立一个数学模型来揭示自变量和因变量之间的关系。这个数学模型通常是一个线性方程，可以表示为y = α + βx，其中y是因变量，x是自变量，α和β是模型的参数。通过对因变量和自变量的实际观测数据进行回归分析，可以求得模型的参数，并利用这个模型进行预测或解释因变量的变化。 在实际应用中，回归分析通常用于解决一些特定的问题。例如，在会计学中，可以使用回归分析来研究两个或多个会计变量之间的关系，以帮助公司进行业绩预测、成本控制和风险管理等方面的决策。此外，回归分析还可以用于市场营销研究、金融风险管理、医学研究等领域。 回归分析的初步应用在教育领域也是非常重要的。教师可以利用回归分析来研究学生学习成绩与各种影响因素之间的关系，以制定更科学的教学计划和教学方法。同时，学生也可以通过学习回归分析方法，提高对因果关系的认识和预测能力，为未来的学习和工作打下坚实基础。 不过，在进行回归分析时，也要注意一些问题。首先，回归分析只能描述变量之间的相关关系，不能说明因果关系。其次，回归分析所建立的数学模型可能存在一定的误差，需要对模型的拟合优度进行检验和修正。最后，回归分析还需要考虑一些统计假设，如线性性、正态性和独立性等，以保证分析结果的有效性。 总之，回归分析是一种重要的统计分析方法，具有广泛的应用前景。通过回归分析，我们可以深入研究不同变量之间的关系，揭示其中的内在规律，并利用这些规律做出科学的预测和决策。希望通过今后的学习和实践，能更好地掌握回归分析方法，发挥其在各个领域的作用，为社会和经济的发展做出更大的贡献。