理解MLP神经网络与BP算法

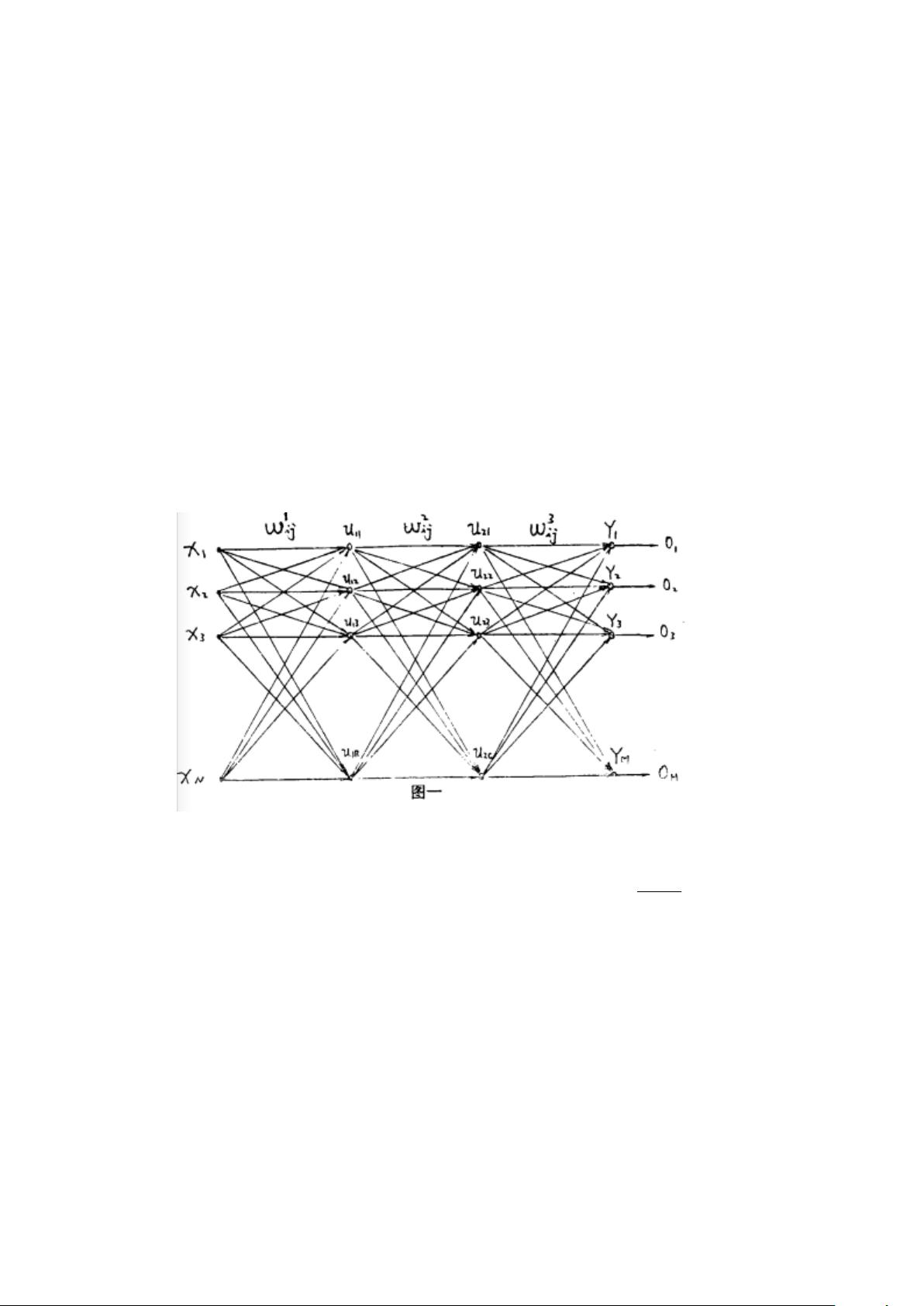
本周的工作重点是深入理解多层感知器（MLP）神经网络，特别是反向传播（BP）算法。通过阅读中国知网上找到的四篇论文，我着重研究了BP算法及其在MLP中的应用。BP算法是训练神经网络的一种常用方法，尤其在解决非线性问题时表现出色。 神经网络是一种基于有向图结构的动态系统，它通过输入信号产生状态响应来处理信息。多层感知器是神经网络的一种，由输入层、输出层和至少一个隐藏层构成，其功能在于通过非线性变换来学习复杂的数据模式。 BP算法在MLP中的工作原理可以分为正向传播和反向传播两个阶段。在正向传播中，输入数据从输入层经过各个隐藏层到输出层，每个节点根据前一层节点的输出计算其自身的输出。对于含有两个隐藏层的模型，第一隐藏层的节点数为B，第二隐藏层的节点数为C，输出层节点数为M。每个节点的输出是其输入与权重的加权和通过激活函数处理的结果。 反向传播阶段，BP算法通过计算误差来更新权重。误差函数E衡量了模型预测值与实际期望值之间的差距，目标是通过调整权重最小化E。对于第K个节点，其误差可通过前一层节点的误差和权重的偏导数得到。这一过程以链式法则递归进行，直到所有层的权重都被更新。 在模型实现中，我们关注以下几点：首先，选择合适的网络结构，比如输入层、隐藏层和输出层的节点数量；其次，初始化权重，通常采用随机值；然后，考虑网络的收敛速度，这可能会影响训练时间和效果；最后，评估算法的优化，论文中提到的优化公式可以改进BP算法的性能。 除了BP算法，论文还提到了共轭梯度法和拟牛顿法作为替代训练策略。共轭梯度法在求解大型稀疏矩阵时效率较高，而拟牛顿法则不需要存储和计算Hessian矩阵，适用于高维度问题。然而，这些方法也存在各自的局限性，如收敛速度可能不如BP算法，或者需要更多的内存。 这一周的学习让我对BP算法及其在MLP中的应用有了更深入的理解，同时也了解了其他优化算法的优缺点。未来，我将继续深入研究这些算法，以提高神经网络模型的训练效率和准确度。