模型阶次辨识方法：从行列式比到Hankel矩阵秩

"模型阶次辨识方法包括利用行列式比、残差的方差、Akaike准则、最终预报误差准则以及Hankel矩阵的秩。这些方法用于估计动态系统的阶次，以构建最合适的数学模型。" 在系统辨识领域，模型阶次辨识是确定一个动态系统模型复杂度的关键步骤。它涉及到找到一个既能准确描述系统行为又不至于过于复杂的模型。以下是几种常用的阶次辨识方法： 1. 利用行列式比估计模型的阶次：行列式比(Det Ratio)是通过比较不同阶次模型的预测误差协方差矩阵的行列式来确定最佳阶次的方法。当阶次n增加时，如果行列式比^DRn与^(n-1)DRn-1相比有显著增加，那么n可能就是接近真实阶次的值。 2. 利用残差的方差估计模型的阶次：这种方法基于假设高阶模型的残差方差应该小于低阶模型。当增加模型阶次时，如果残差方差不再明显减小，说明模型可能已经过拟合，此时的阶次被认为是合适的。 3. Akaike信息准则(AIC)：AIC是一种衡量模型复杂度和拟合优度的统计量，它在惩罚复杂模型的同时考虑了模型的预测能力。阶次选择的目标是使AIC达到最小，因为较小的AIC值意味着模型在复杂性和拟合度之间找到了较好的平衡。 4. 最终预报误差准则(FPE)：FPE是基于模型的预报误差平方和的期望值，它同样会随着模型阶次的增加而减小。当FPE的增长不再显著时，对应的阶次被视为合适的阶次。 5. Hankel矩阵的秩估计模型的阶次：Hankel矩阵是描述系统动态特性的一种工具，其秩反映了系统的最小阶次。通过计算不同阶次Hankel矩阵的秩，当秩不再增加时，可以推断出系统的实际阶次。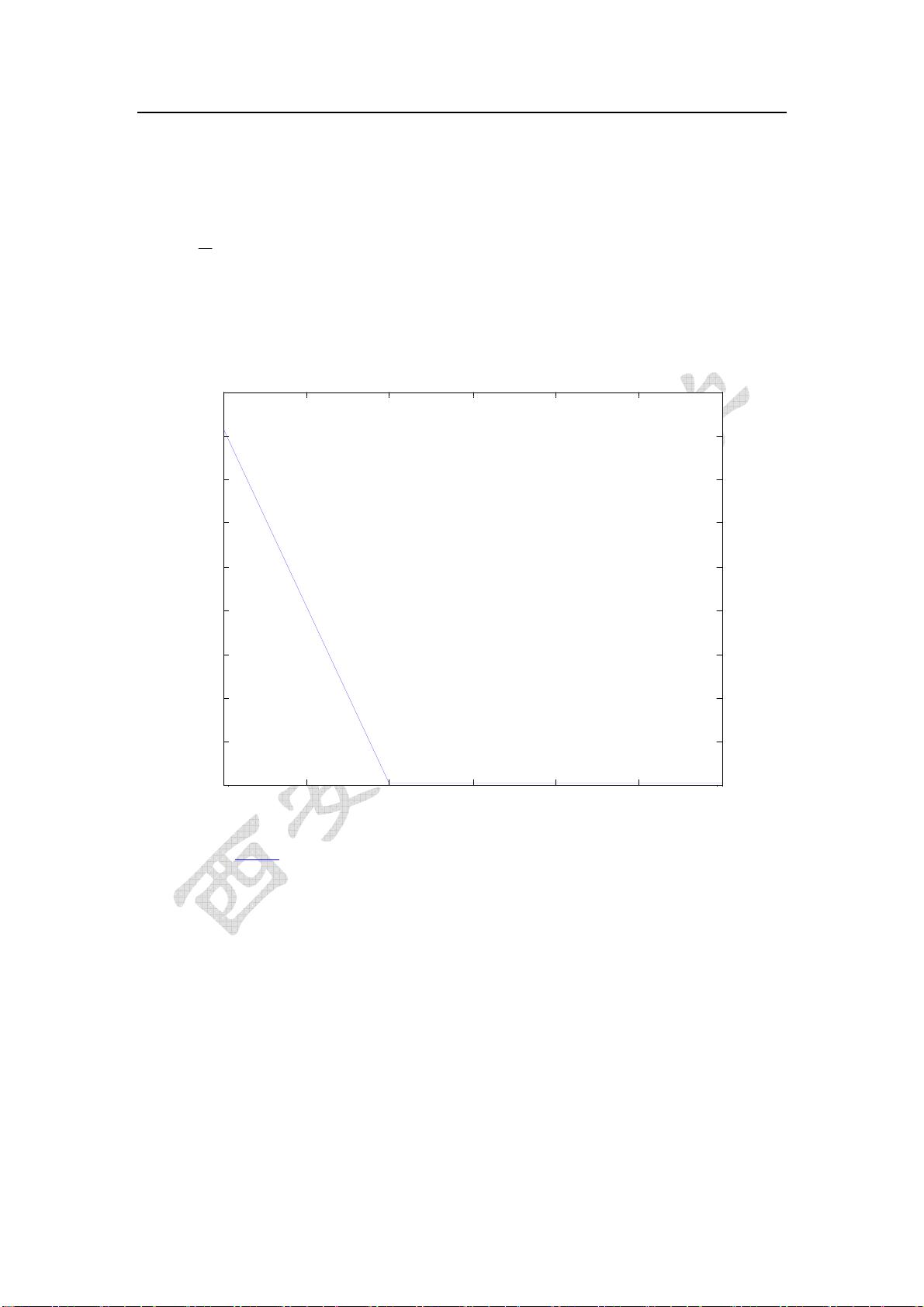 在实际应用中，可能会结合使用多种方法来验证和确认模型阶次，以确保模型的稳定性和准确性。例如，文中提到的例子展示了如何通过行列式比来识别模型阶次，随着阶次n的增加，行列式比DRn的变化可以帮助我们找到一个转折点，这个转折点的阶次通常是系统的实际阶次。在给定的例子中，随着n的增加，DRn的值经历了显著增长，从而帮助我们确定了合适的模型阶次。