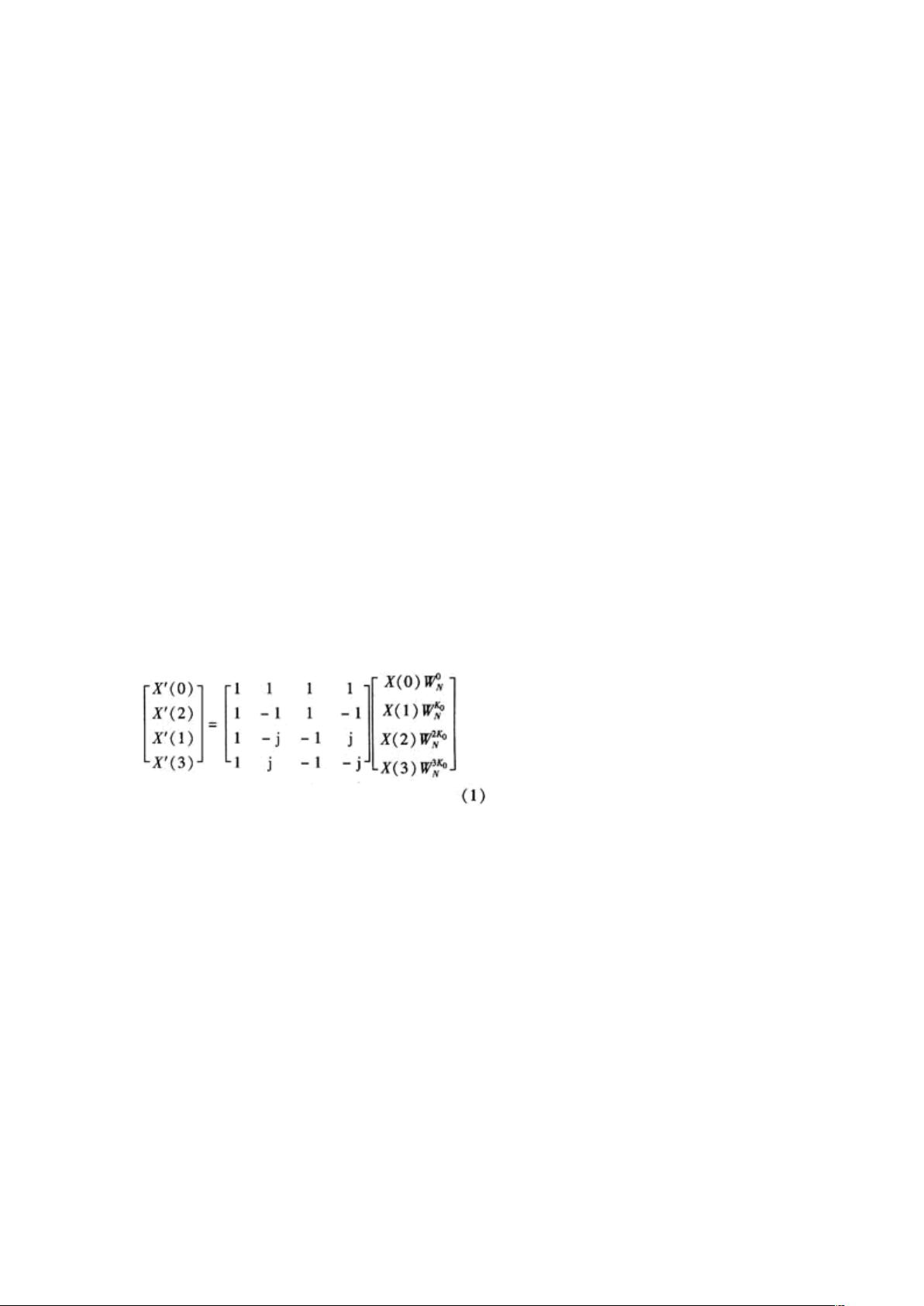FPGA实现的高效基4-FFT算法与1024点设计详解

基于FPGA的高速流水线FFT算法实现是一种利用现场可编程门阵列(FPGA)技术来加速有限长序列离散傅立叶变换(DFT)计算的过程。FPGA因其灵活性、高速度和可编程特性，成为实施FFT的理想平台，尤其是基4-FFT算法，因为其运算效率相对较高且控制结构较为简单。 基4-FFT算法的核心是4点DFT，通过递归分割和并行处理，将1024点的DFT分解为5级蝶形运算。每一级蝶形运算独立进行，例如第一级有256个蝶形运算，每级结束后数据会原址存入RAM，以备下一级处理。这种设计显著减少了存储需求，仅需两个1k×16 bits的RAM单元即可满足。 设计的关键组成部分包括： 1. 双口RAM：用于存储输入和处理后的数据，实部和虚部各用一个1k×16 bits的RAM，提供了高效的数据存储和访问。 2. 蝶形运算单元：负责执行基4的蝶形操作，这是FFT算法中的核心步骤，通过复数乘法和加法实现信号频率成分的交换。 3. 旋转因子生成模块：利用预设的正弦和余弦查找表，根据算法需要实时生成旋转因子，确保每次运算的正确性。 整个1024点FFT算法模块设计注重了硬件资源的有效利用和运算过程的并行性，通过流水线方式提高计算速度。相比于基2-FFT，虽然基4-FFT的运算量较大，但通过优化结构和硬件实现，能够在FPGA上实现高速、高效的性能。此外，该设计还考虑了输出的有效数据区间标志，以便用户知道何时可以信任输出结果，进一步提升了系统的实用性。 总结来说，基于FPGA的高速流水线FFT算法实现通过结合FPGA的并行计算能力、精心设计的算法结构以及高效的存储管理，成功地提高了DFT计算的性能，适用于对实时性和计算效率要求高的频谱分析和滤波器设计等应用场景。