BSP树详解：概念、应用与构建方法

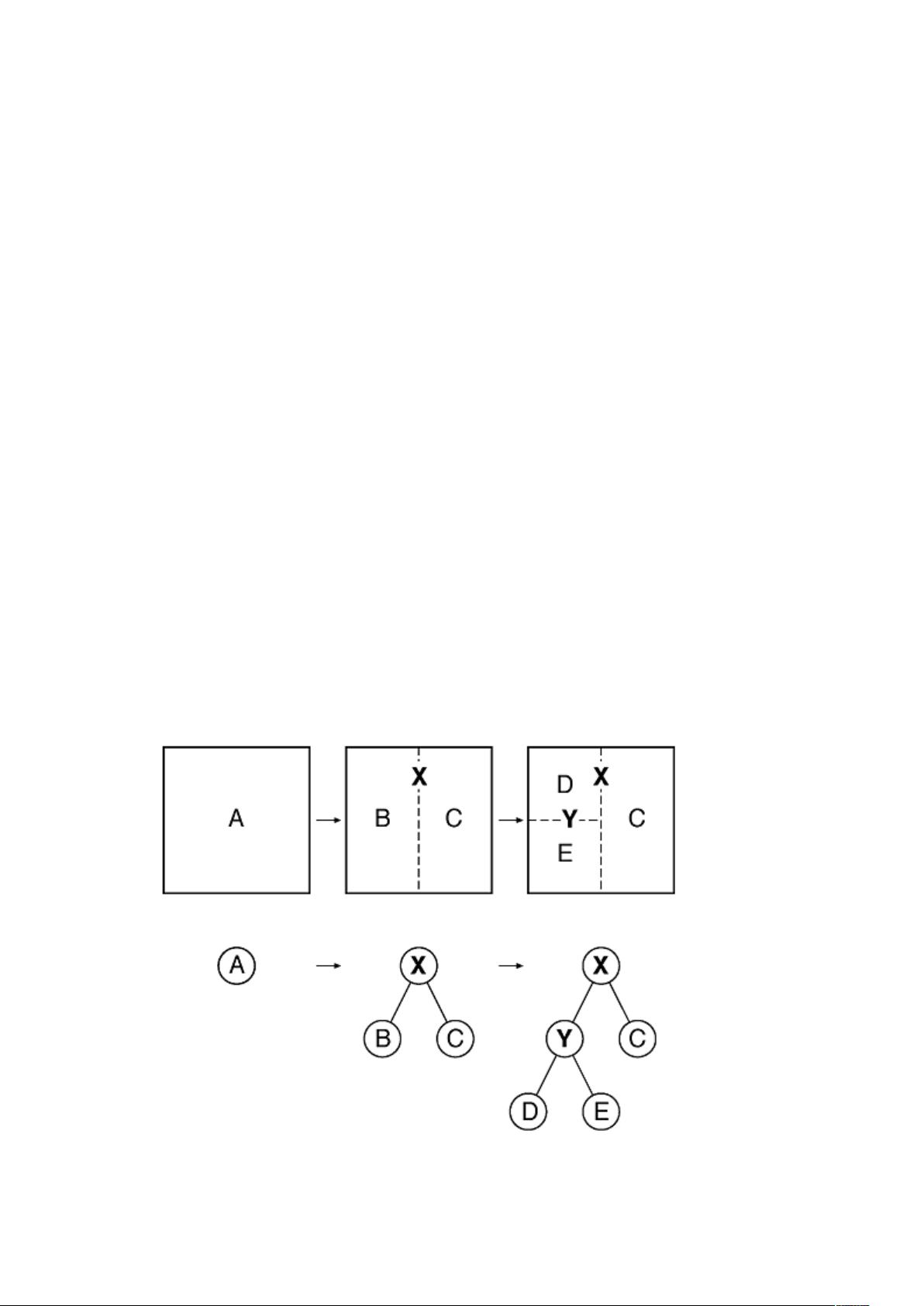
"本文主要介绍了BSP树的基本概念和应用，包括二维和三维空间中的示例，以及构建BSP树的步骤。BSP树是一种用于N维空间元素排序和查找的二叉树，尤其适用于图形处理和实体建模等领域。" BSP树，全称为Binary Space Partitioning Tree（二进制空间分割树），是一种数据结构，主要用于组织和操作多维空间中的几何对象。在BSP树中，每个节点代表一个凸子空间，并由一个超平面分割，超平面是N-1维的对象，如二维空间中的直线，三维空间中的平面。这种分割方式使得BSP树能够有效地对空间中的元素进行排序和查找。 在二维空间的例子中，BSP树通常用于处理线段，通过选取分割平面（例如X轴或Y轴）将空间划分为对等的部分。随着递归过程的进行，空间会被不断细分，形成一个层次结构。在三维空间中，BSP树可以用于处理多边形，比如在计算机图形学中用于隐藏面剔除和光线追踪等任务。 构建BSP树的过程分为几个关键步骤： 1. **选择分割平面**：分割平面的选择取决于BSP树的具体应用和多边形的排列。可以选择多边形所在平面，或者坐标轴垂直的平面。平衡BSP树通常更优，但可能导致多边形需要被分割。 2. **分割多边形集合**：根据选择的分割平面，将多边形分为两组。完全位于分割平面一侧的多边形放入相应子集，与分割平面相交的多边形则需要被切割后再分配。 3. **确定停止条件**：构建BSP树的递归终止条件通常与应用场景相关，可能是节点包含的多边形数量达到一定阈值，或者达到预设的深度限制。 BSP树的这些特性使其在各种领域中有广泛的应用，比如游戏中的碰撞检测、场景管理，机器人路径规划，以及CAD软件中的实体建模等。然而，构建BSP树时需要注意避免过于复杂的分割，这可能导致树结构过于深，影响性能。因此，选择合适的分割策略和平衡树的方法是优化BSP树的关键。 BSP树是一种强大的工具，它利用二叉树结构对空间进行有组织的划分，从而提高在多维空间中执行查找和操作的效率。理解BSP树的概念及其构建方法，对于理解和解决涉及几何对象处理的问题至关重要。