"初中数学知识点总结：有理数、数轴、相反数、绝对值、大小比较"

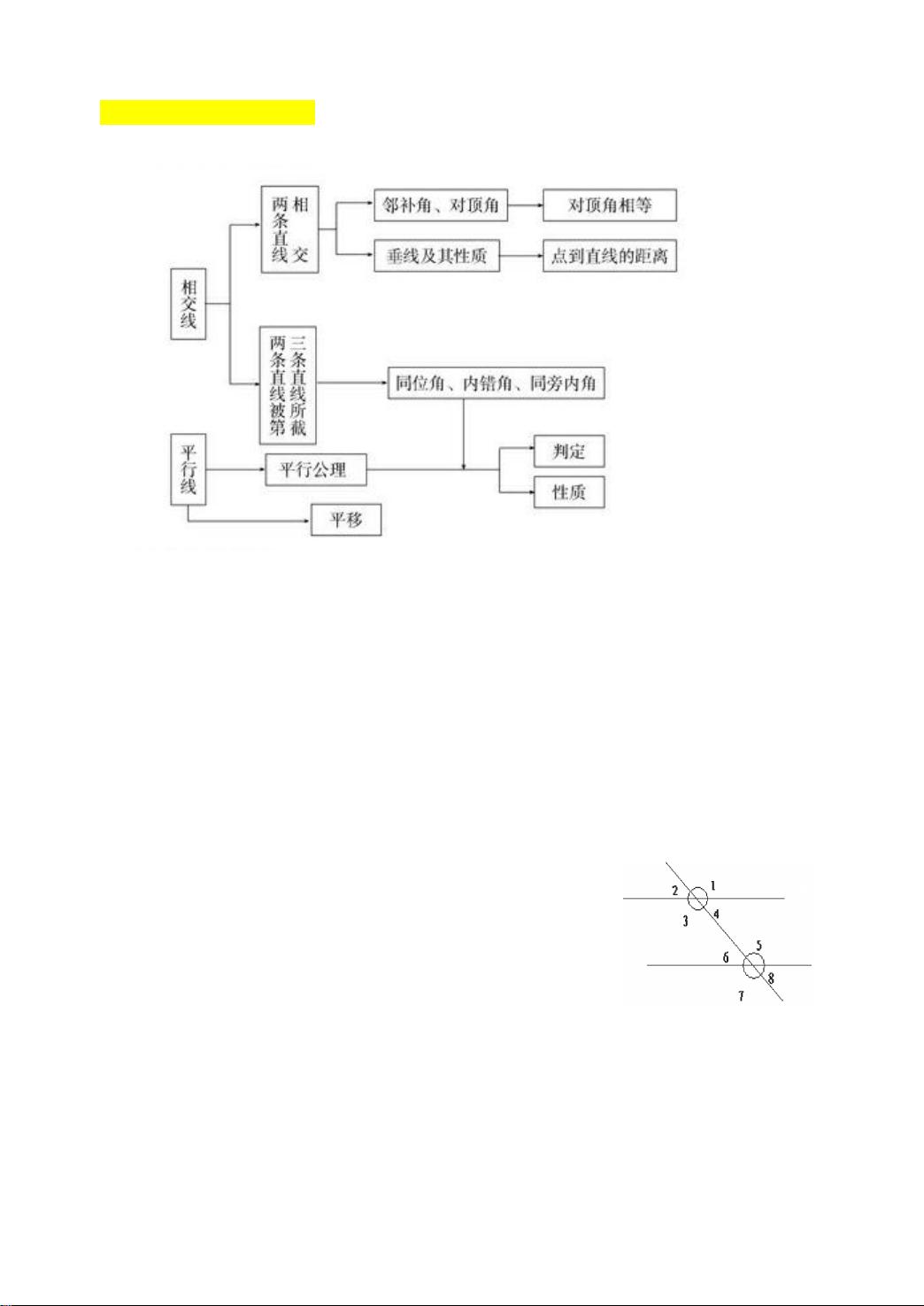
初中数学知识点总结 第一章 有理数 一．知识框架 在初中数学中，有理数是一个重要的概念，它包括了整数、分数、零和负数。数轴是用来表示有理数的一种工具。相反数和绝对值也是有理数中常见的概念。在比较有理数的大小时，我们需要注意它们的正负和绝对值的大小关系。 二．知识概念 1. 有理数 有理数是一类可以用分数的形式表达的数，它包括整数、分数、正数、负数和零。有理数可以用以下形式表示：m/n，其中m和n都是整数且n不等于0。有理数可以分为以下几类： ① 负有理数：这是一个负数的有理数，它可以用分数的形式表示为-（m/n）。 ② 整数：这是一个不带小数部分的有理数，它可以用分数的形式表示为m/1。 ③ 正有理数：这是一个正数的有理数，它可以用分数的形式表示为m/n。 注意：0既不是正数也不是负数，-a不一定是负数，a也不一定是正数，π不是有理数。 2．数轴 数轴是一条直线，其中包含了原点、正方向和单位长度，用来表示并比较有理数的大小。在数轴上，我们可以根据有理数的位置来判断它们的大小关系。 3．相反数 相反数指的是符号相反但绝对值相等的两个数。对于任意一个有理数a，它的相反数是-b，其中b是a的绝对值。特别的，0的相反数还是0。两个有理数的和为0的充分必要条件是它们互为相反数。 4．绝对值 绝对值是一个数在数轴上与原点的距离，在数轴上表示某个数的点与原点的距离，我们称之为该数的绝对值。对于任意一个有理数a，它的绝对值可以表示为以下形式： ① 当a为正数时，|a| = a ② 当a为负数时，|a| = -a ③ 当a为0时，|a| = 0 绝对值经常在问题中进行分类讨论。 5．有理数比大小 在比较有理数的大小时，我们需要考虑它们的正负和绝对值的大小。一般来说： ① 正数的绝对值越大，这个数越大。 ② 负数的绝对值越大，这个数越小。 ③ 相同符号的数，绝对值大的数大；不同符号的数，正数大于负数。 ④ 零和其他数比较时，零是最小的整数。 以上就是初中数学中有理数的一些重要知识点。掌握了这些概念，我们就能更好地理解数学问题，进行数学计算，解决实际生活中的问题。