经典排序算法详解：C++实现与特性对比

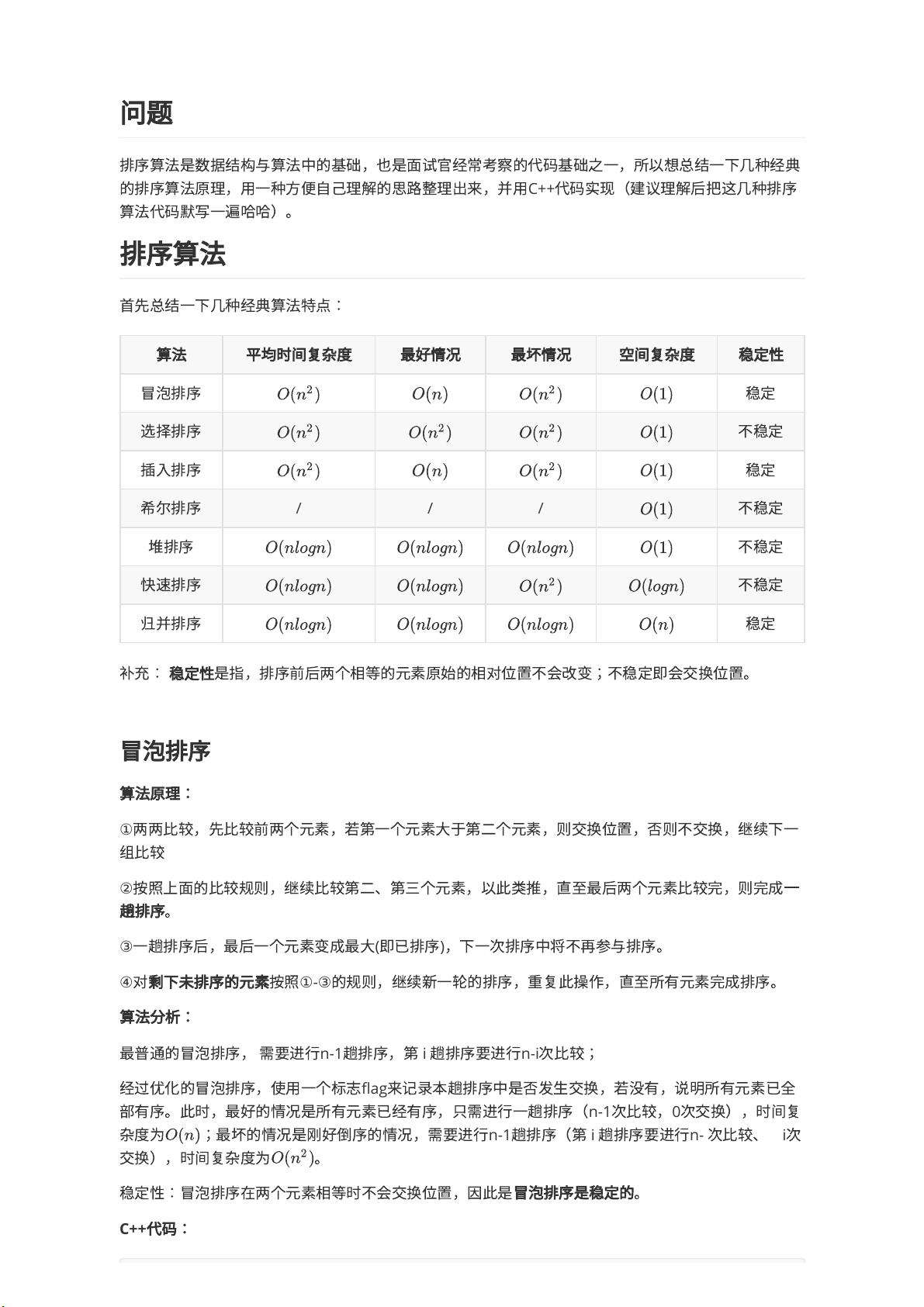
本文档主要介绍了6种经典的排序算法：冒泡排序、选择排序、插入排序、希尔排序、堆排序、快速排序和归并排序。排序算法是数据结构与算法的基础，对于面试者来说是一项重要的技能。 1. 冒泡排序：这是一种简单的排序方法，通过不断比较相邻元素并交换它们的位置，使得最大（或最小）的元素逐渐“浮”到序列的末尾。冒泡排序分为n-1趟，每趟进行n-i次比较，最坏情况时间复杂度为O(n^2)。特点是稳定，即相等元素的相对位置不变。 2. 选择排序：每次从未排序的部分选择最小（或最大）元素，将其放到已排序部分的末尾。无论序列有序还是无序，选择排序都会进行n-1趟，每趟n-i次比较，时间复杂度始终为O(n^2)，且不稳定，如例子[4,5,6,4,3,2]排序后，相等元素的位置发生改变。 3. 插入排序：将元素逐个插入到已排序序列的正确位置。它在处理近乎有序的序列时效率较高，最坏情况下时间复杂度为O(n^2)，但最好情况下为O(n)，是一种稳定的排序方法。 4. 希尔排序：基于插入排序，通过调整增量序列来优化性能。虽然希尔排序不是稳定的，但其平均时间复杂度在一定程度上优于简单插入排序，适合大量数据。 5. 堆排序：利用堆这种数据结构实现的排序，通过构建大顶堆或小顶堆进行排序，时间复杂度最坏情况下为O(n log n)，但不稳定。 6. 快速排序：采用分治法，选取一个基准值，将数组分为两部分，一部分小于基准，一部分大于基准，再对这两部分递归地进行排序。平均时间复杂度为O(n log n)，但最坏情况下为O(n^2)，不稳定。 7. 归并排序：也是一种分治法，将数组分为两半，分别排序后再合并。归并排序具有稳定性和O(n log n)的时间复杂度。 总结这些排序算法，除了考虑时间复杂度和稳定性外，还有空间复杂度（如冒泡排序原地排序，空间复杂度为O(1)，而归并排序需要额外的空间）。理解这些排序算法的工作原理和特性有助于在实际编程中根据场景选择合适的排序方法。通过实际编写代码，能够加深对这些算法的理解和记忆。